前言
以下算法的是实现,BFS、DFS是基于图的邻接表存储方式实现的, A*基于图的邻接矩阵存储
BFS
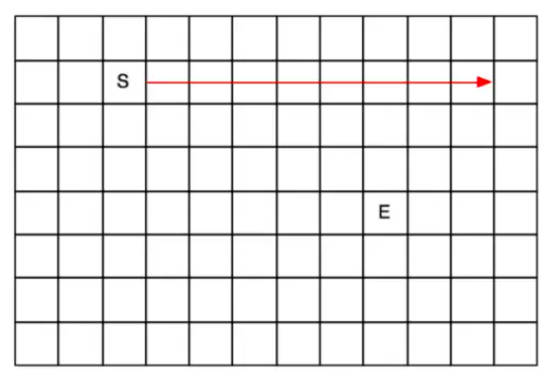
BFS,广度优先遍历,其遍历的形式可以理解为树的层次遍历,直到找到对应的节点,然后停止。所以,可以通过一个队列来实现该算法。
package com.wkk.utils;
import com.wkk.graph.LGraph;
import org.omg.CORBA.INTERNAL;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
/**
* @Time: 20-3-20下午3:16
* @Author: kongwiki
* @Email: kongwiki@163.com
*/
public class BFS {
// 图使用邻接表进行存储
private boolean[] marked;
private int[] edgeTo;
private final int s;
public BFS(LGraph graph, int s) {
marked = new boolean[graph.V()];
edgeTo = new int[graph.V()];
this.s = s;
bfs(graph, s);
}
private void bfs(LGraph graph, int s) {
Queue<Integer> queue = new LinkedList<Integer>();
queue.offer(s);
marked[s] = true;
while (!queue.isEmpty()){
Integer v = queue.poll();
for (Integer element : graph.adj(v)) {
if(!marked[element]){
edgeTo[element] = v;
marked[element] = true;
queue.offer(element);
}
}
}
}
// 判断是否存在路径 s ---> v
public boolean hasPathTo(int v){
return marked[v];
}
// 存储s--->v的路径
public Stack<Integer> pathTo(int v){
if (!hasPathTo(v)) {return null;}
Stack<Integer> path = new Stack<Integer>();
for (int x = v; x != s; x = edgeTo[x]) {
path.push(x);
}
path.push(s);
return path;
}
}
总结
BFS算法能够找到 s —-> v路径中的最优解
DFS
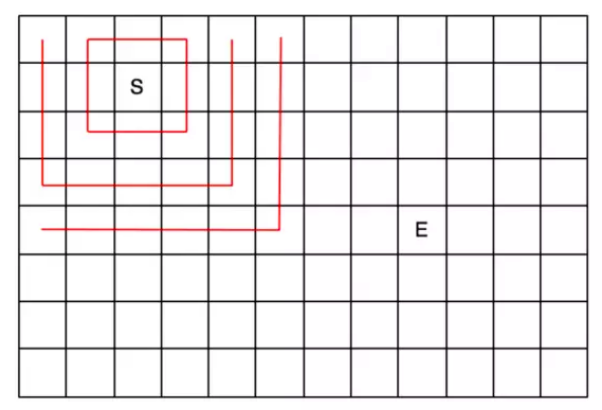
关于dfs, 其应用范围很广,譬如可以解决排列组合问题等等等。首先,会从开始节点朝某一个方向进发,直到遇到边界或者障碍物,才回溯。dfs算法需要一个栈进行从存储所扫描路径上的所有节点,递归其本身也是一个栈的使用, 所以完全可以使用递归实现DFS算法。
public class DFS {
private boolean[] marked;
private int count;
public DFS(LGraph graph, int v){
marked = new boolean[graph.V()];
dfs(graph, v);
}
public void dfs(LGraph graph, int v){
marked[v] = true;
count++;
for (Integer w : graph.adj(v)) {
if(!marked[w]){
dfs(graph, w);
}
}
}
public boolean marked(int w){
return marked[w];
}
public int count(){
return count;
}
}
总结
DFS算法存在问题有:
- 路径不可能是最优解
- 寻路时间比较长
A*
官方定义
A*搜索算法(A* search algorithm)是一种在图形平面上,有多个节点的路径,求出最低通过成本的算法。其应用非常的广,主要分为两大应用,第一就是游戏中的NPC的移动计算,第二就是地图导航的应用。简而言之,其就是一种寻路算法。
该算法综合了最良优先搜索和Dijkstra算法的优点:在进行启发式搜索提高算法效率的同时,可以保证找到一条最优路径(基于评估函数)。

A*算法的评估函数,其中$ g(n) $表示从起点到任意顶点n的实际距离,$h(n)$ 表示任意顶点$ n$ 到起点的估算距离。
$ f(n) = g(n) + h(n) $
这个公式遵循以下特性:
- 如果$g(n)$为0,即只计算任意顶点$n$到目标的评估函数$h(n)$而不计算起点到顶点$n$的距离,则算法转化为使用贪心策略的最良优先搜索,速度最快,但可能得不出最优解;
- 如果$h(n)$不大于顶点$n$到目标顶点)的实际距离,则一定可以求出最优解,而且$h(n)$越小,需要计算的节点越多,算法效率越低,常见的评估函数有——欧几里得距离、曼哈顿距离、切比雪夫距离;
- 如果$ h(n) $为0,即只需求出起点到任意顶点的$ n $最短路径$ g(n) $,而不计算任何评估函数$ h(n) $,则转化为单源最短路径问题,即Dijkstra算法,此时需要计算最多的顶点;
以上的摘自维基百科,一些名词可能有些抽象,现做举例说明;
实例讲解
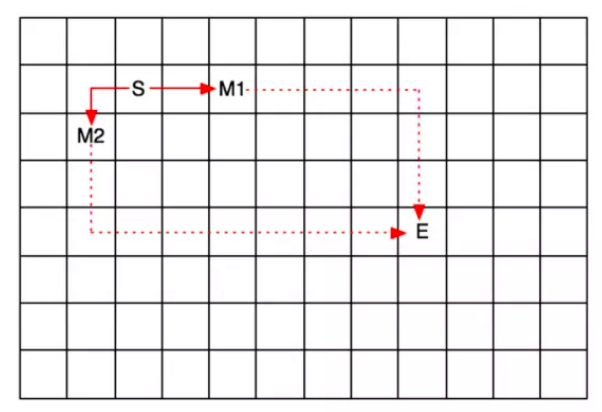
对于上图,从顶点s出发,均走了两步,分别到达了M1和M2,接下来应该选择哪条路线到达终点E,很明显,选择M1这条路, 因为从M1出发,到E的距离终于7步,比从M2出发到E的距离9步,要少。
回想刚才的思路,发现,我们不仅思考了从起始点到当前点的距离, 还考虑了当前点到终点的距离。这就是A*算法的核心。其相比于BFS算法,除了考虑中间某个点到出发点的距离以外,还考虑了这个点同目标点的距离。这就是A*算法比广度优先算法智能的地方。也就是所谓的启发式搜索。实例中的s 到M1的距离就是g(n), M1到E的距离就是h(n)
对于上述的公式, g(n)是已知的,但是h(n)是需要进行计算的。 对于h(n)的精确计算,可以按照刚才实例的方式,使用横向距离+纵向距离的方式进行计算(曼哈顿距离),理论上来说是可行的,但是遇到如下的问题,那么使用刚才的方式计算h(n)的精确值就是错误的了
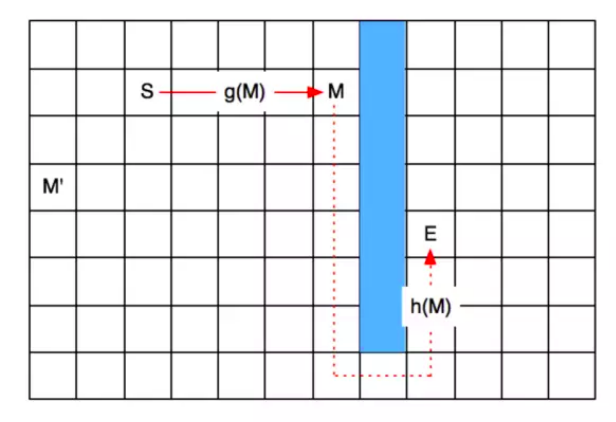
因为有障碍物,M到E的就需要绕过这个障碍物。但是,我们完全没有必要计算h(n)的精确的值,只需要尽可能找那些f(n)=g(n)+h(n)小的点(其中h(n)是个估算值),当做我们的路径经过点,即使实际的h'(n)值可能和h(n)值不等也没关系,我们就当做一个参考(总比广度优先搜索好)。如果通过这个估算,能干掉很多明显很差的点,我们也就节省了很多不必要的花销。
比如,上图中, M点即使是绕路,也比M'点要强。在估算的时候,我们就可以将S左边的点基本上都抛弃掉,从而减少我们扩展的点数,节约计算的时间。
经过上述的分析,接下来就只需要解决如下的两个问题:
这个估算的函数h(M)怎么样去计算?
- 曼哈顿距离
- 欧式距离
- 切比雪夫距离
- …
对于不同的估算函数h(M)来讲,对于我们的搜索结果会有什么样的影响?
h'(n)=h(n)- 也就是每次扩展的那个点我们都准确的知道,如果选他以后,我们的路径距离是多少,这样我们就不用乱选了,每次都选最小的那个,一路下去,肯定就是最优的解,而且基本不用扩展其他的点
h'(n) < h(n)我们到最后一定能找到一条最短路径(如果存在另外一条更短的评估路径,就会选择更小的那个),但是有可能会经过很多无效的点。极端情况,当h==0的时候,最终的距离函数就变成:
f(n)=g(n)+h(n) => f(n)=g(n)+0 => f(n)=g(n)这也就是
BFS算法。
h'(n) > h(n)- 有可能就很快找到一条通往目的地的路径,但是却不一定是最优的解。
总结
A*算法最后留给我们的,就是在时间和距离上需要考虑的一个平衡。如果要求最短距离,则一定选择h小于等于实际距离;如果不一定求解最优解,而是要速度快,则可以选择h大于等于实际距离。
实现思路
思路
(如果有路径)采用结点与结点的父节点(前一个节点) 的关系从最终结点回溯到起点,得到路径。
定义
$ f(n) = g(n) + h(n) $的实现
$g(n)$的实现方式:
计算方式有挺多种的,这里我们就用这种吧,假设每个结点代表一个正方形,横竖移动距离:斜移动距离=1 : 1.4($\sqrt(2)$),我们取个整数10和14吧,也就是说当前结点G值=父节点的G+(10或14)。
$ h(n)$的实现方式:
曼哈顿距离
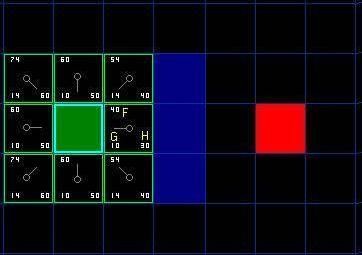
- 每个方块代表一个节点,
- 方块中左下角为
g(n) - 方块中右下角为
h(n) - 方块中左上角为
f(n)
辅助表:Open、Close列表
在A算法中,需要使用两个辅助表来记录结点。 一个用于记录可被访问的结点,称为Open表;一个是记录已访问过的结点,称为Close表。 *这两个表决定了算法的结束:条件是最终结点在Close表中(找到路径)或Open表为空(找不到了路径)。
移动结点、相邻结点的处理
每次从Open表中取出F值最小的结点出来(这里我们使用优先队列来处理比较好),作为当前结点;然后将当前结点的所有邻结点按照邻结点规则加入到Open表中;最后将当前结点放入Close表中,这里就是每次循环的执行内容。
邻结点规则:
- 当邻结点不在地图中,不加入Open表
- 当邻结点是障碍物,不加入Open表
- 当邻结点在Close表中,不加入Open表
- 当邻结点不在Open中,加入Open表,设该邻结点的父节点为当前结点
- 当邻结点在Open表中,我们需要做个比较:如果邻结点的G值>当前结点的G值+当前结点到这个邻结点的代价(10或14),那么修改该邻结点的父节点为当前的结点(因为在Open表中的结点除了起点,都会有父节点),修改G值=当前结点的G值+当前结点到这个邻结点的代价
- 如果邻结点的G值<当前结点的G值+当前结点到这个邻结点的代价(10或14), 如果没有一条路径可以通过使用当前格子得到改善,所以我们不做任何改变。
步骤
把起始格添加到开启列表。
重复如下的工作:
a) 寻找开启列表中F值最低的格子。我们称它为当前格。
b) 把它切换到关闭列表。
c) 对相邻的8格中的每一个?
- 如果它不可通过或者已经在关闭列表中,略过它。反之如下。
- 如果它不在开启列表中,把它添加进去。把当前格作为这一格的父节点。记录这一格的F,G,和H值。
- 如果它已经在开启列表中,用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。如果是这样,就把这一格的父节点改成当前格,并且重新计算这一格的G和F值。如果你保持你的开启列表按F值排序,改变之后你可能需要重新对开启列表排序。
d) 停止,当你
- 把目标格添加进了开启列表,这时候路径被找到,或者
- 没有找到目标格,开启列表已经空了。这时候,路径不存在。
保存路径。从目标格开始,沿着每一格的父节点移动直到回到起始格。这就是你的路径。
实现代码
输入涉及数据结构:
代表地图二值二维数组(0表示可通路,1表示路障)
int[][] maps = { { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 }, { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 }, { 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0 }, { 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 }, { 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0 }, { 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0 }, { 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 }, { 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 }, { 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 }, { 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 }, };坐标类
public class Coord { /** * 坐标原点在左上角 所以y是高 x是宽 * y向下递增 x向右递增 * 将x和y封装成一个类 方便传参 * 重写equals方法比较坐标(x,y)是不是同一个。 */ public int x; public int y; public Coord(int x, int y) { this.x = x; this.y = y; } @Override public boolean equals(Object obj) { if (obj == null) { return false; } if (obj instanceof Coord) { Coord c = (Coord) obj; return x == c.x && y == c.y; } return false; } }Node类
public class Node implements Comparable<Node> { // 坐标 public Coord coord; // 父结点 public Node parent; // G:是个准确的值,是起点到当前结点的代价 public int G; // H:是个估值,当前结点到目的结点的估计代价 public int H; public Node(int x, int y) { this.coord = new Coord(x, y); } public Node(Coord coord, Node parent, int g, int h) { this.coord = coord; this.parent = parent; G = g; H = h; } // 方便优先队列排序。 public int compareTo(Node o) { if (o == null) { return -1; } if (G + H > o.G + o.H) { return 1; } else if (G + H < o.G + o.H) { return -1; } return 0; } }A*算法输入的数据结构的封装
package com.wkk.a; /** * @Time: 20-3-21上午12:35 * @Author: kongwiki * @Email: kongwiki@163.com */ public class MapInfo { // 二维数组的地图 public int[][] maps; //地图的宽 public int width; // 地图的高 public int hight; // 起始结点 public Node start; // 最终结点 public Node end; public MapInfo(int[][] maps, int width, int hight, Node start, Node end) { this.maps = maps; this.width = width; this.hight = hight; this.start = start; this.end = end; } }
处理:
几个常量:二维数组中哪个值表示障碍物、二维数组中绘制路径的代表值、计算G值需要的横纵移动代价和斜移动代价。
// 障碍值 public final static int BAR = 1; // 路径 public final static int PATH = 2; // 横竖移动代价 public final static int DIRECT_VALUE = 10; // 斜移动代价 public final static int OBLIQUE_VALUE = 14;定义两个辅助表:Open表和Close表。Open表的使用是需要取最小值,使用优先队列PriorityQueue,Close只是用来保存结点,没其他特殊用途,就用ArrayList。
// 优先队列(升序) Queue<Node> openList = new PriorityQueue<Node>() List<Node> closeList = new ArrayList<Node>();定义几个布尔判断方法:最终结点的判断、结点能否加入open表的判断、结点是否在Close表中的判断。
/** * 判断结点是否是最终结点 */ private boolean isEndNode(Coord end, Coord coord) { return coord != null && end.equals(coord); } /** * 判断结点能否放入Open列表 */ private boolean canAddNodeToOpen(MapInfo mapInfo, int x, int y) { // 是否在地图中 if (x < 0 || x >= mapInfo.width || y < 0 || y >= mapInfo.hight) { return false; } // 判断是否是不可通过的结点 if (mapInfo.maps[y][x] == BAR) { return false; } // 判断结点是否存在close表 if (isCoordInClose(x, y)) { return false; } return true; } /** * 判断坐标是否在close表中 */ private boolean isCoordInClose(Coord coord) { return coord != null && isCoordInClose(coord.x, coord.y); } /** * 判断坐标是否在close表中 */ private boolean isCoordInClose(int x, int y) { if (closeList.isEmpty()) { return false; } for (Node node : closeList) { if (node.coord.x == x && node.coord.y == y) { return true; } } return false; }回溯绘制路径
/** * 在二维数组中绘制路径 */ private void drawPath(int[][] maps, Node end) { if (end == null || maps == null) { return; } System.out.println("总代价:" + end.G); while (end != null) { Coord c = end.coord; maps[c.y][c.x] = PATH; end = end.parent; } }
运行结果
自定义Graph
int[][] maps = {
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0 },
};
开始节点为:(1,1)
结束节点为: (9, 5)
输出结果:
总代价:176
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 2 2 2 2 2 2 2 2 2 2 2 2 0 0
0 0 1 1 0 0 0 0 0 0 1 1 1 2 0
0 0 0 1 0 0 0 0 0 1 1 2 2 0 0
0 0 0 1 1 1 1 1 1 1 2 0 0 0 0
0 0 0 1 0 0 1 0 0 2 0 0 0 0 0
0 0 0 1 0 0 0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0 1 0 0 0 0 0 0
待优化
int类型 —-> 泛型
异常数据处理