堆排序

堆排序

堆排序在 top K 问题中使用比较频繁，并且经常被用来实现优先级队列。堆排序是采用二叉堆的数据结构来实现的，虽然实质上还是一维数组。二叉堆是一个近似完全二叉树 。

堆的定义如下：

1. $L(i) \leq L(2i)$ 且 $L(i) \leq L(2i+1)$ (小根堆)
2. $L(i) \geq L(2i)$且 $L(i) \geq L(2i+1)$ （大根堆）

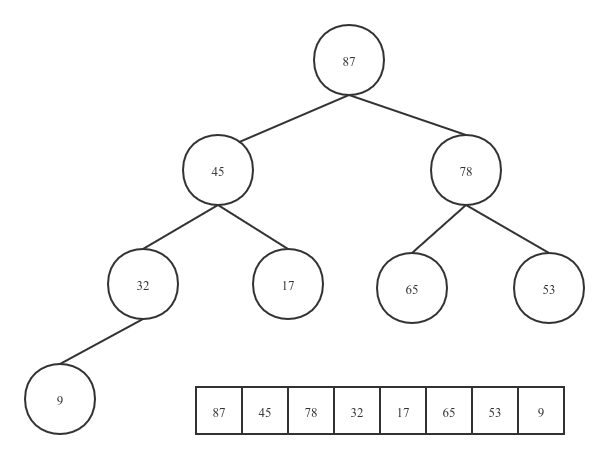
大根堆示意图.png

堆排序的关键是构造初始堆，对初始序列建堆，就是一个反复筛选的过程，因为是近似于完全二叉树，所以从第$\lfloor n/2 \rfloor$为根的子树开始调整（对于大根堆，根节点的关键字和其左右子女中关键字相比较大的进行交换）之后依次对各个节点$\lfloor n/2 \rfloor -1 ～ 1$为根的子树进行筛选。

实例

对关键字序列：53、17、 78、 9、 45、 65、 87 、32 构建大根堆

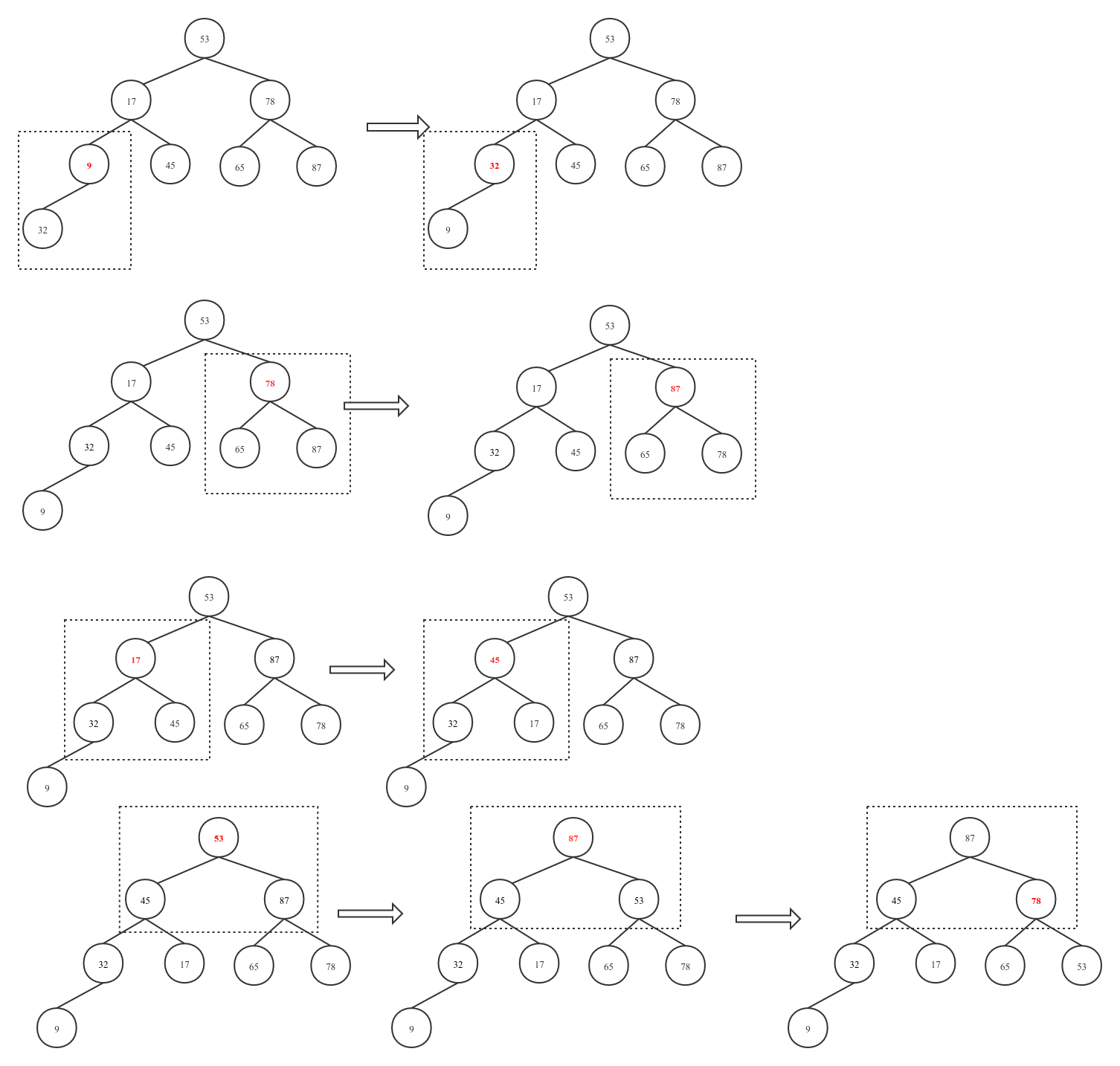
大根堆的构建.png

插入

插入是从尾部插入(当前堆有n个元素，在第n+1位置中插入)，然后调整

删除

删除是从根节点开始删除，删除之后再进行调整

Java代码实现

public void buildMaxHeap(int[] nums) {
    int length = (nums.length - 1) / 2;
    // 从n/2开始构建初始堆
    for (int i = length; i >= 0; i--) {
        adjustDown(nums, i, nums.length-1);
    }
}
private void adjustDown(int[] nums, int k, int len) {
    nums[0] = nums[k];
    // 以第k个节点为根的子树进行调整
    for (int i = 2 * k; i <= len; i *= 2) {
        // 寻找子树中的最值
        if(i < len && nums[i] < nums[i+1]){
            i ++;
        }
        if(nums[0] >= nums[i]){
            break;
        }
        else {
            nums[k] = nums[i];
            k = i;
        }
    }
    nums[k] = nums[0];
}