TODO

前言

矩阵树定理的理解，且代码实现。并且添加了几道实战题目

简介&思路

Kirchhoff 矩阵树定理（简称矩阵树定理）解决了一张图的生成树个数计数问题。

无向图

设$G$是一个有n个顶点的无向图。定义度数矩阵$D(G)$为：

$D{ii}(G) = \mathrm{deg}(i), D{ij} = 0, i\neq j$

G的邻接矩阵$A(G)$为：

$A{ij}(G) = A{ij}(G)$

定义 Laplace 矩阵（亦称 Kirchhoff 矩阵）$L$为：

$L(G) = D(G) - A(G)$

$G$的所有不同的生成树的个数等于其Laplace矩阵（$L(G)$）的任何一个n-1主子式的绝对值，所谓 n-1 阶主子式,就是对
于 r(1≤r≤n),将$G$的第 r 行、第 r 列同时去掉后得到的新矩阵$G_r$

举例：

无向图$G$如下图所示

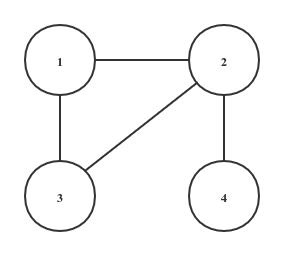
图论.png

则$A(G)$表示为：

$\begin{matrix}0 & 1 & 1 & 0\\ 1 & 0 & 1 & 1\\ 1 & 1 & 0 & 0\\ 0 & 1 & 0 & 0\\\end{matrix} $

$D(G)$表示为:

$\begin{matrix}2 & 0 & 0 & 0\\ 0 & 3 & 0 & 0\\ 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 1\\\end{matrix} $

$L(G)$表示为：

$\begin{matrix}2 & -1 & -1 & 0\\ -1 & 3 & -1 & -1\\ -1 & -1 & 2 & 0\\0&-1&0&1\\ \end{matrix} $

去除$r$ = 1之后得到主子式$G_r$的绝对值即为该图的生成树个数。

$G_r$ = $\begin{matrix} 3 & -1 & -1 \\-1&2&0\\-1&0&1\\ \end{matrix} $ 根据公式计算的 $|G_r|$ = 3

所以该图共有三种生成树。

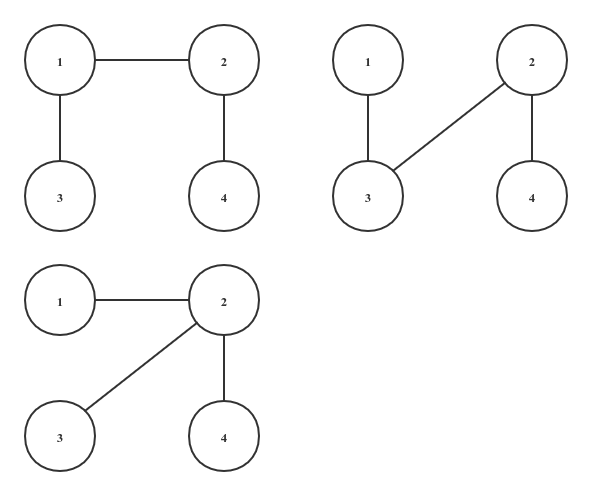
生成树个数.png
生成树个数.png

是不是很神奇， 我也觉得很神奇，然后去看了证明，也很神奇😑

有向图同理

同理

行列式的变换

  1. 交换两行/列位置，行列式取相反数
  2. 对一行/列乘以某数，行列式也乘以某数
  3. 用一行的倍数减去另一行，行列式的值不变
  4. 一个上三角行列式的值等于对角线的乘积
  5. 转置矩阵，行列式不变

ACM矩阵行列式计算

实现

按照数学公式计算余子式的值的话，复杂度达到$O(N!)*N $ ，所以需要通过行列式的性质，进行基础的变换之后再计算。

题目

  1. 「HEOI2015」小 Z 的房间
  2. 「FJOI2007」轮状病毒

小Z的房间

矩阵树定理的裸题，题目给定的限制为1≤n,m≤9

矩阵维度限制在了个位数，算法有待优化。

#include <cstdio>
#include <iostream>
#include <cmath>
using namespace std;
typedef long long LL;
const int N = 100;
const LL mod = 1e9;
int n, m, ed;
LL ans = 1;
int h[N][N], vis[N];
LL f[N][N];
char s[N];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%s", s);
        for (int j = 0; j < m; j++)
            if (s[j] == '.')
                h[i][j + 1] = 1;  //记录下房间的位置
            else
                vis[(i - 1) * m + j + 1] = 1;  //重要！！为墙的行一定全为0！！
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++)
            if (h[i][j]) {  //若为房间
                ed = 0;     //纪录度数矩阵
                if (h[i][j - 1])
                    f[(i - 1) * m + j][(i - 1) * m + j - 1] = -1, ed++;  //左
                if (h[i][j + 1])
                    f[(i - 1) * m + j][(i - 1) * m + j + 1] = -1, ed++;  //右
                if (h[i - 1][j])
                    f[(i - 1) * m + j][(i - 2) * m + j] = -1, ed++;  //上
                if (h[i + 1][j])
                    f[(i - 1) * m + j][i * m + j] = -1, ed++;  //下
                f[(i - 1) * m + j][(i - 1) * m + j] = ed;      //加上度数矩阵
            }
    }
    n = n * m - 1;  //删去最后一行最后一列，并计算行列式的大小
    for (int i = 1; i <= n; i++)
        if (!vis[i]) {  //注意！ 非墙的才继续
            for (int j = i + 1; j <= n; j++)
                if (!vis[j])           //同上
                    while (f[j][i]) {  //辗转相除
                        LL r = f[i][i] / f[j][i];
                        for (int k = 1; k <= n; k++)
                            f[i][k] = (f[i][k] - f[j][k] * r % mod + mod) % mod, swap(f[i][k], f[j][k]);
                        ans = (mod - ans) % mod;  //交换两行，答案取负
                    }
            if (f[i][i] == 0) {
                puts("0");
                return 0;
            }                                   //若主对角线有0，则答案为0
            ans = (ans * f[i][i] + mod) % mod;  //计算答案
        }
    printf("%lld\n", ans);
}

一下是测试结果

矩阵树定理-小Z的房间.png
矩阵树定理-小Z的房间.png

轮状病毒

总结

引用周东老师的结束语吧：

扎实的数学功底是解决问题的保证,创造性地联想是解决问题的灵魂。

References