简介

AVL树的引入是因为BST在极端的情况下，会退化为链表，那么查找的时间从$O(logN)$ —-> $O(N)$

AVL树是一种自平衡的二叉树，定义如下

  1. BST
  2. 左、右子树高度差的绝对值不超过1(平衡因子Balance Factor)
    空树、左右子树都是AVL
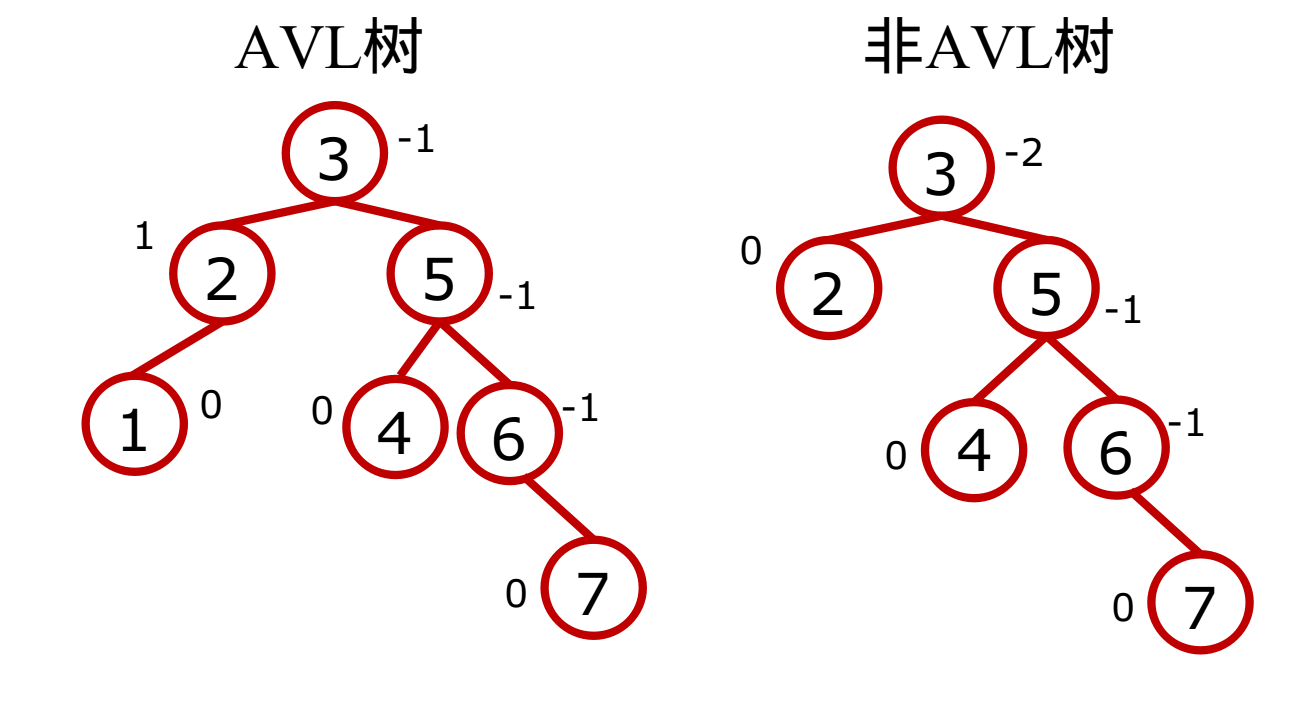
AVL树.png
AVL树.png

插入&旋转

三节点单旋转

左旋

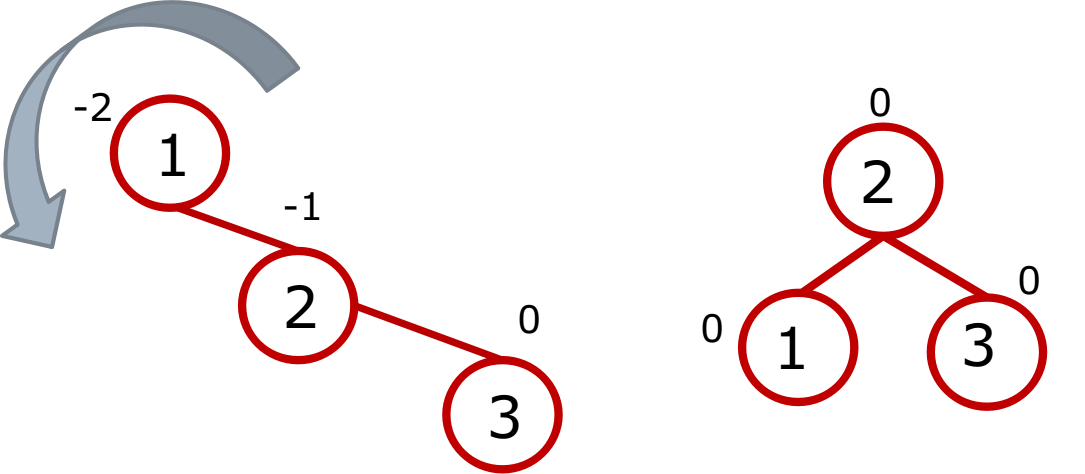
AVL_左旋.png
AVL_左旋.png

右旋

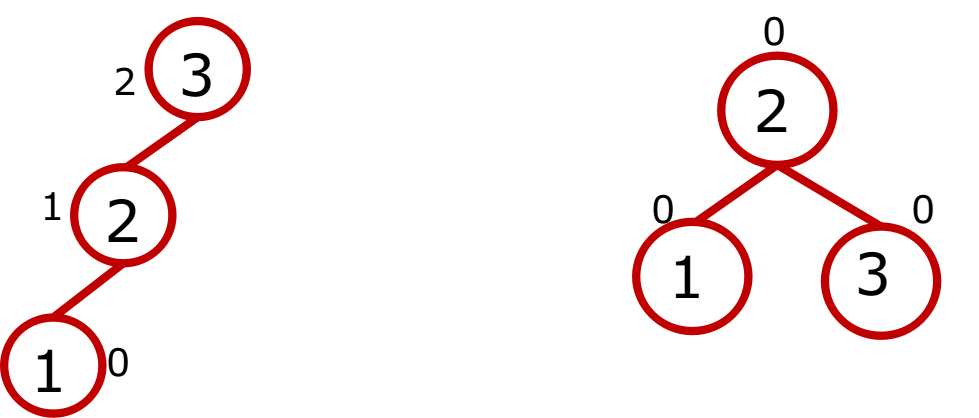
AVL_右旋.png
AVL_右旋.png

三节点双旋转

LR旋转

AVL_LR.png
AVL_LR.png

RL旋转

同理

什么时候需要旋转

插入关键字key后，节点p的平衡因子由原来的1或者-1，变成了2或者-2，则需要旋转；只考虑插入key到左子树left的情形，即平衡因子为2

  1. 情况1：key<left.key, 即插入到left的左子树，需要进行单旋转，将节点p右旋

  2. 情况2：key>left.key, 即插入到left的右子树，需要进行双旋转，先将left左旋，再将p右旋

插入到右子树right、平衡因子为-2，完全对称

情况1

AVL_插入_情况1.png
AVL_插入_情况1.png

情况2

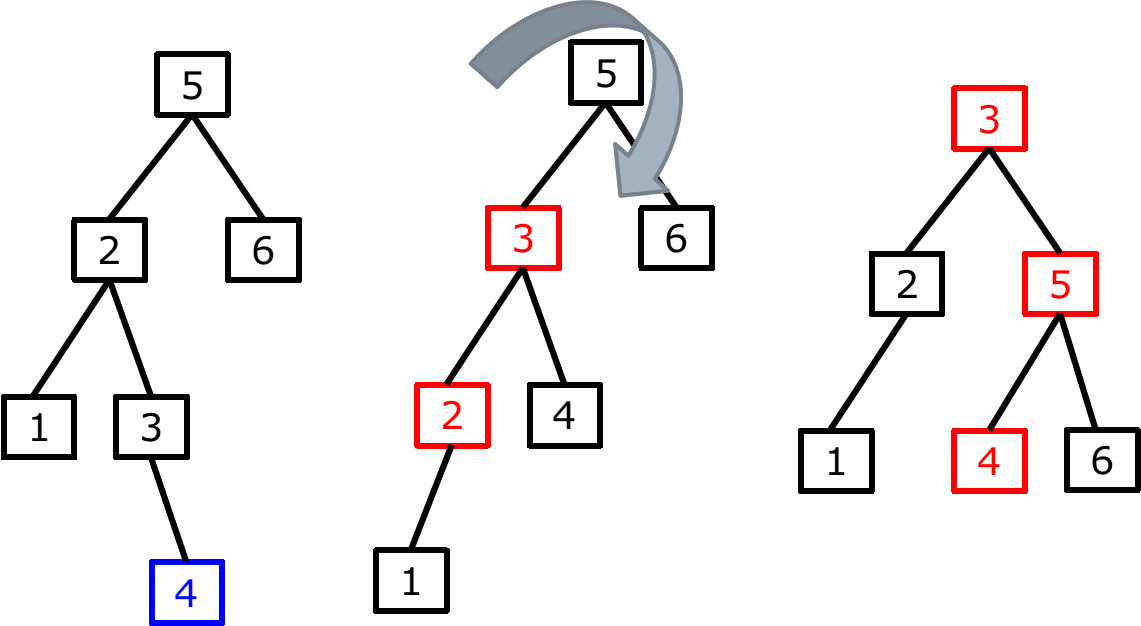
AVL_插入_情况2_1.png
AVL_插入_情况2_1.png

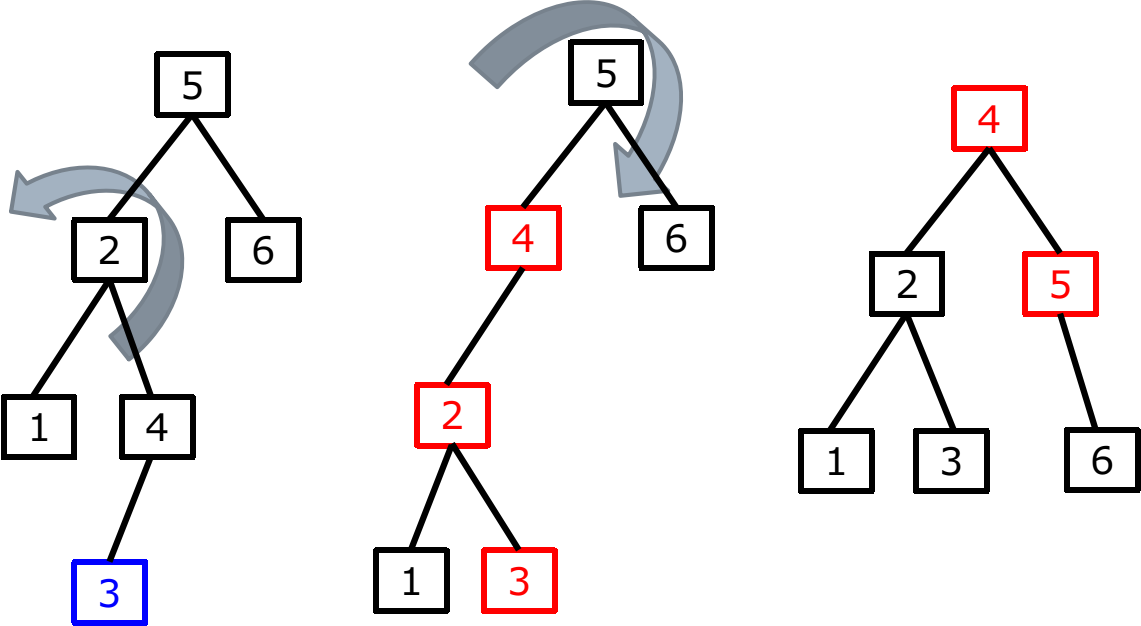
AVL_插入_情况2_2.png

删除

类似插入，假设删除了p右子树的某个节点，引起了p的平衡因子d[p]=2，分析p的左子树left，三种情况如下：

  1. 情况1：left的平衡因子d[left]=1，将p右旋
  2. 情况2：left的平衡因子d[left]=0，将p右旋
  3. 情况3：left的平衡因子d[left]= -1，先左旋left，再右旋p

删除左子树，即d[p]= -2的情形，与d[p]=2对称

情况1

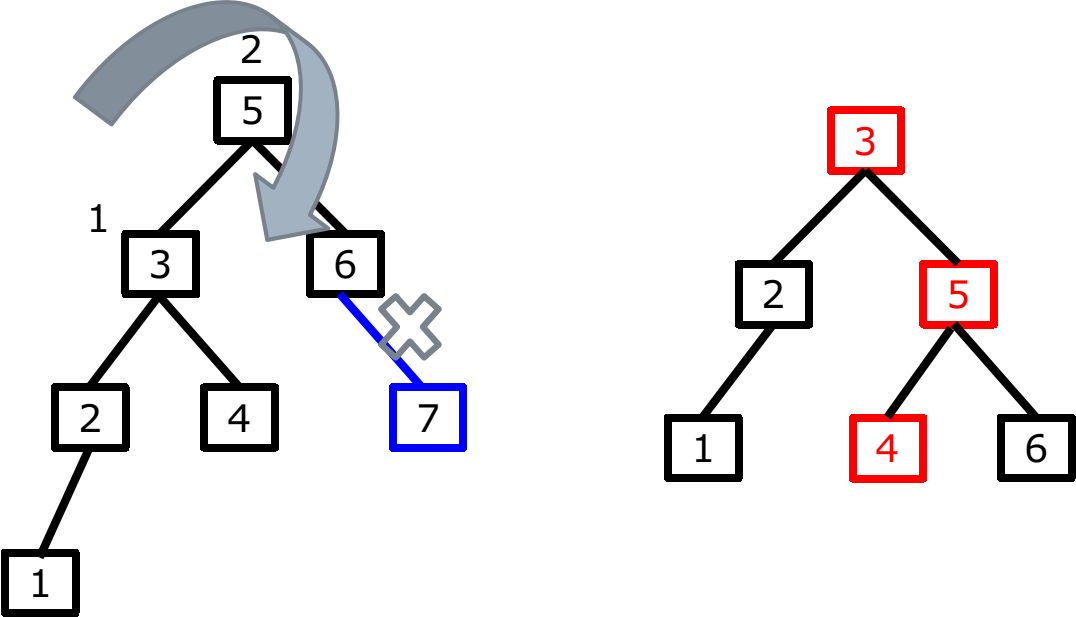
AVL_删除_情况1.png
AVL_删除_情况1.png

情况2

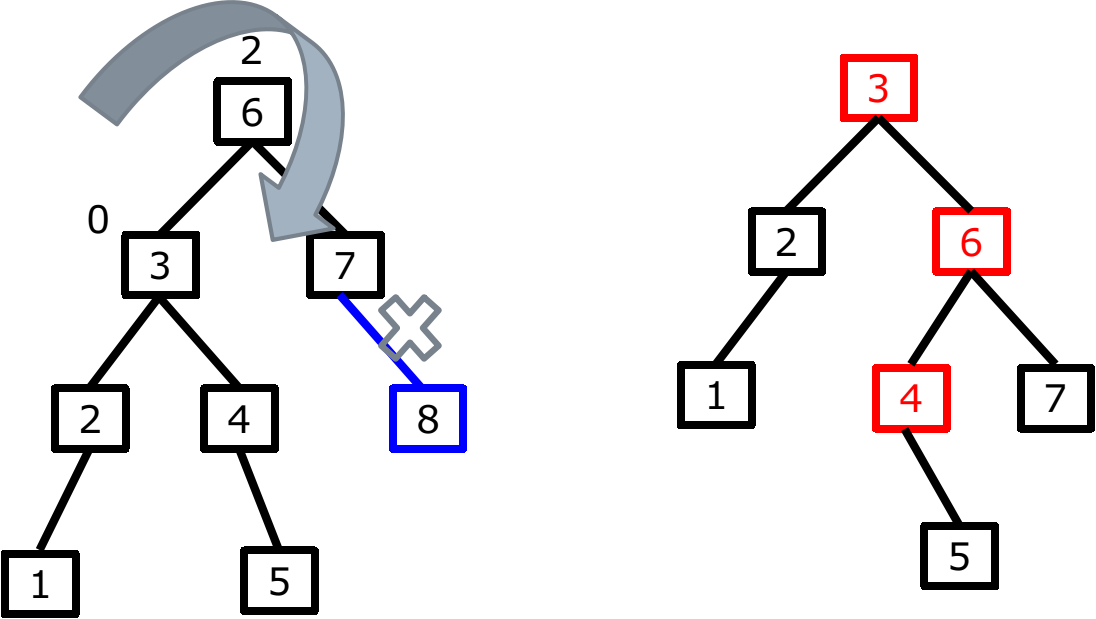
AVL_删除_情况2.png
AVL_删除_情况2.png

情况3

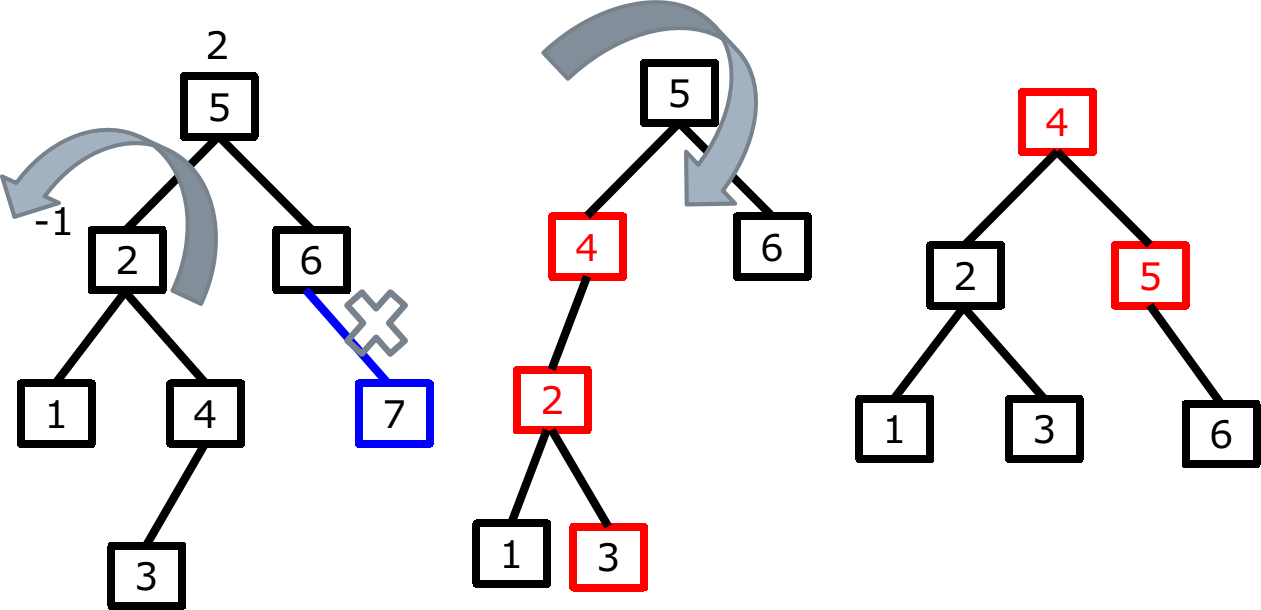
AVL_删除_情况3.png
AVL_删除_情况3.png

面试

排序数组（链表）转AVL

108. Convert Sorted Array to Binary Search Tree

109. Convert Sorted List to Binary Search Tree

判断是否为平衡二叉树

LeetCode 110. Balanced Binary Tree

相关题目会持续添加

References