B树

共分为两个部分， 首先是B的性质、B树的建立、插入和删除，之后是B+树性质、以及相比于B树，区别在哪儿

B树的性质

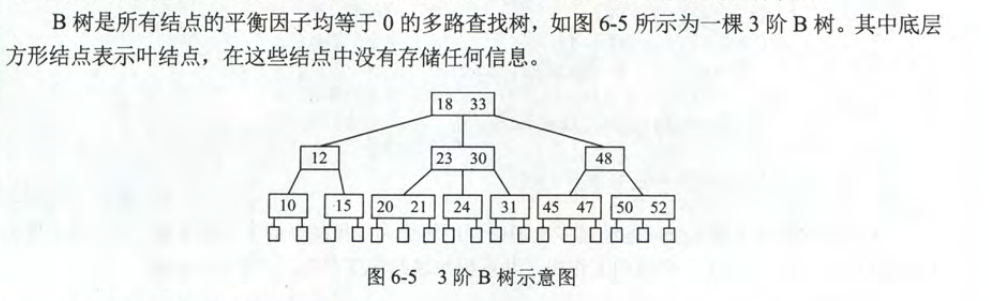
B树又称为多路平衡查找树，B树中所有结点的孩子结点数的最大值称为B树的阶。通常使用m表示。

一颗m阶B树或为空，或为满足如下特性的m叉树。

  1. 树中每个节点至多有m颗子树（m-1关键字）

  2. 若是根节点不是终端节点，至少有两颗子树

  3. 除根以外的所有非叶子节点至少 $\lceil m/2 \rceil$ 颗子树（$\lceil m/2 \rceil $ -1 关键字）

  4. 所有的非叶子结点的结构如下：

    b树节点信息.png

  1. 所有叶子节点都出现在同一层次上，并且不带任何信息
b树示例.png
b树示例.png

B树的高度

$ n$ : 关键字的个数

$h \le log_\lceil m/2 \rceil ((n+1)/2) + 1 $

具体的证明，百度。。。

B树的查找

因为其是有序的，其和二叉搜索树的查找类似，只不过不同的是每个节点其有多个关键字的有序表，然后根据该节点的子树做多路分支决定。

基本步骤

  1. 在B树中找到节点
  2. 在节点内找到关键字

由于B树通常是存储在磁盘上的， 所有第一次是在磁盘上进行， 之后第二次在内存中运行，即在找到目标节点之后，将其储存内存之后， 然后使用顺序查找或者折半查找，查找等于K的关键字。

B树的插入、B树的删除

可根据参考书和可视化网站进行理解

B树每个节点的关键字个数范围 $[\lceil m/2 \rceil -1 , m-1]$

其中删除的操作共分为两种情况，并且这两种情况又有细分

删除关键字k为非终端节点（终端节点 != 叶子节点）

其实和AVL的删除是如出一辙的

  1. 小于k的子树中关键字的个数 > $\lceil m/2 \rceil -1$ 则找出k的前驱k’替代k， 再递归的删除k‘
  2. 大于k的子树中关键字的个数 > $\lceil m/2 \rceil -1$ 则找出k的后继k’替代k， 再递归的删除k’
  3. k的左右子树的关键字个数 均为 $\lceil m/2 \rceil-1$ 则进行合并两个子树，然后删除k即可

删除关键字k为终端节点

  1. 如果k所在的节点关键字个数> $\lceil m/2 \rceil -1$ 直接删除

  2. k所在的节点关键字个数=$\lceil m/2 \rceil -1$

    1. 兄弟够借

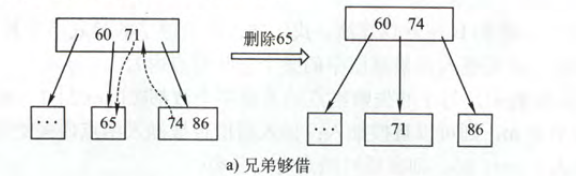
      b树-兄弟够借.png

    2. 兄弟不够借

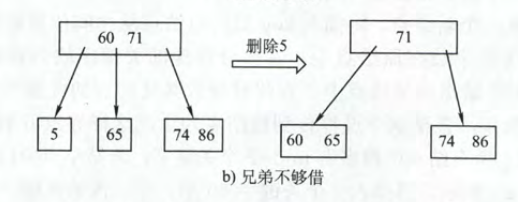
      b树-兄弟不够借.png

B+树

B+树的性质

B+树是应数据库的所需， 所出现的一种B树的变形

一颗m阶的B+树需满足下列条件

  1. 每个分支节点最多有m颗子树
  2. 非叶子的根节点至少有两颗子树，其他的分支节点至少有$\lceil m/2 \rceil $ 颗子树
  3. 节点的子树个数和关键字个数相等
  4. 所有叶子节点包含所有关键字及指向相应记录的指针，并且叶子节点将关键字按大小顺序排列，并且相邻叶节点按大小顺序相互链接起来
  5. 所有分支节点中仅包含它的各个子节点中关键字的最大值和指向该子树的指针

B+树结构示意图

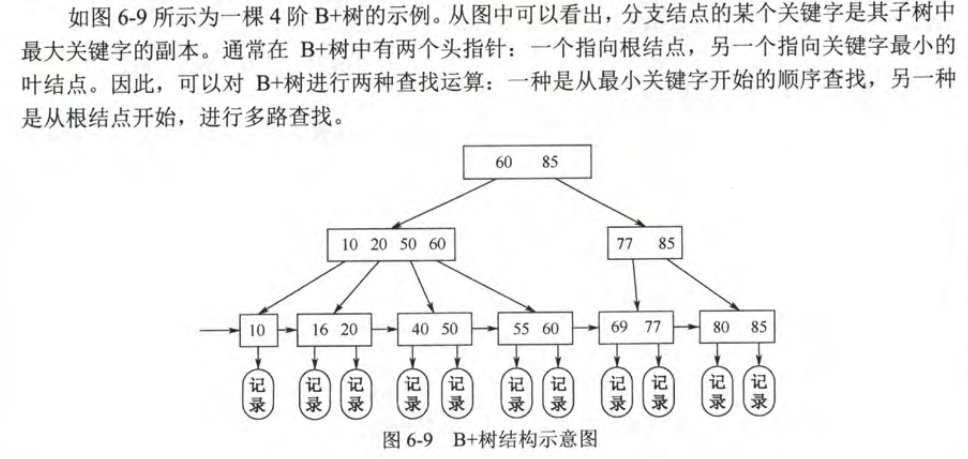
B_树结构示意图.png
B_树结构示意图.png

B+树的性质II：

才发现，原来各种资料上关于B+树的性质，不经相同….. 以下为维基百科的定义

和王道的定义区别不大，但是分支节点关键字个数比子树个数小1， 也就是和B的节点定义一样。

1）B+树包含2种类型的结点：内部结点（也称索引结点）和叶子结点。根结点本身即可以是内部结点，也可以是叶子结点。根结点的关键字个数最少可以只有1个。

2）B+树与B树最大的不同是内部结点不保存数据，只用于索引，所有数据（或者说记录）都保存在叶子结点中。

3） m阶B+树表示了内部结点最多有m-1个关键字（或者说内部结点最多有m个子树），阶数m同时限制了叶子结点最多存储m-1个记录。

4）内部结点中的key都按照从小到大的顺序排列，对于内部结点中的一个key，左树中的所有key都小于它，右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。

5）每个叶子结点都存有相邻叶子结点的指针，叶子结点本身依关键字的大小自小而大顺序链接。

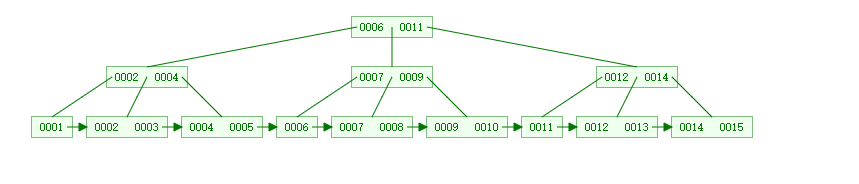
B+树结构示意图II

下图为一个三阶B+树的示意图

B_树结构示意图.png
B_树结构示意图.png

B和B+区别

B+ trees don’t store data pointer in interior nodes, they are ONLY stored in leaf nodes. This is not optional as in B-Tree. This means that interior nodes can fit more keys on block of memory and thus fan out better.

The leaf nodes of B+ trees are linked, so doing a linear scan of all keys will requires just one pass through all the leaf nodes. A B tree, on the other hand, would require a traversal of every level in the tree. This property can be utilized for efficient search as well, since data is stored only in leafs.

  1. B+内部节点不存储数据，只有叶子节点存储信息，B树没有，这也就意味着，B+树比B树的内部节点能存储更多的信息
  2. B+树叶节点的数据是链接的，可做一次线性扫描获取所有的数据， 但是B树就需要遍历整个B树

查找、插入、删除

B+和B树相同，但是对于查找而言，如果非叶子节点上关键字值等于给定值时，并不终止，而是继续查找，直到找到叶子节点上的该关键字为止。所以，B+树的查找，无论成功与否，每次都是一条从根节点到叶子节点的路径。

reference