BST详解

简介

BST有很多的名字，如二叉排序树、二叉搜索树、Binary Sort Tree、Binary Search Tree、BST
其具有如下性质：

1. 定义空树是一个BST
2. 左子树所有结点的值均小于根结点的值
3. 右子树所有结点的值均大于根结点的值
4. 左右子树都是BST(递归定义)
5. 中序遍历序列为升序

查找

假设查找关键字key

1. 若根结点的关键字值等于key，成功
2. 若key小于根结点的关键字，递归查找左子树
3. 若key大于根结点的关键字，递归查找右子树
4. 若子树为空，查找不成功

插入

按照元素的大小进行查找，与查找类似。然后插入到对应的位置（插入到当前BST的叶子节点）

删除

假设删除节点p，其父节点为f，分如下3种情况进行讨论：

1. p是叶子节点，直接删除
2. p只有左子树left(右子树right)，直接用p.left(p.right)替换p
3. p既有左子树left，又有右子树right，找到右子树的最小节点rightMin(找到left的最大节点leftMax)，用rightMin(leftMax)的值替换p的值，再根据以上两种情况删除rightMin(leftMax)

P是叶子节点

bst_删除_情况1.png

P只有左子树或右子树

bst_删除_情况2.png

P既有左子树又有右子树

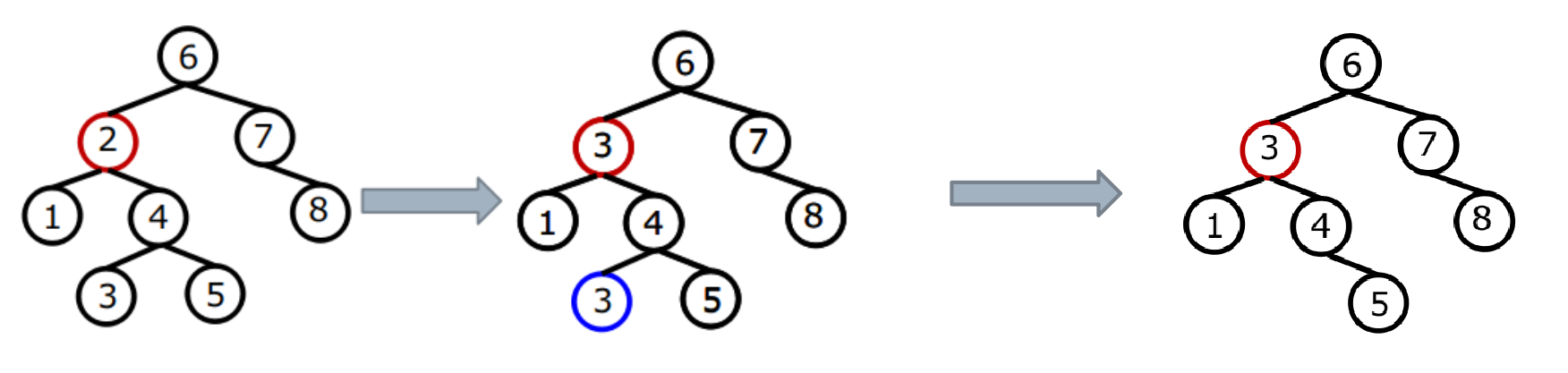
bst_删除_情况3.png

面试汇总

给定一个BST的节点，寻找以当前节点为根节点的最值

private static TreeNode getLastEntry(TreeNode node) {
    while (node.right != null) {
        node = node.right;
    }
    return node;
}
private static TreeNode getFirstEntry(TreeNode node) {
    while (node.left != null) {
        node = node.left;
    }
    return node;
}

给定节点t，后继(前驱)节点

1. t为最值节点

   • 无前驱或后继

2. 当t有右子树

   • 直接寻找其右子树最小节点（左子树最大节点）即可
3. t无右子树
   1. 向上回溯，找到第一个孩子是左子树孩子（右子树孩子）的父亲p
   2. 向上回溯，找到第一个关键字比孩子大（小）的父亲p（利用BST特性）

LintCode448. Inorder Successor in BST

使用指针代替路径栈，将空间复杂度降到O(1)

栈是自底向上寻找结果，指针为自顶向下寻找结果

public static TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
    if (root == null) {
        return null;
    }
    // 情况0: 本身就是最值
    if (getLastEntry(root) == p) {
        return null;
    }
    // 情况1: 有右子树
    if (p.right != null) {
        return getFirstEntry(p.right);
    }
    // 情况2: 没有右子树
    TreeNode parent = root;
    // temp指针代替栈
    TreeNode temp = root;
    while (parent != null) {
        if (parent == p) {
            break;
        } else if (parent.val > p.val) {
            temp = parent;
            parent = parent.left;
        } else {
            parent = parent.right;
        }
    }
    return temp;
}
private static TreeNode getLastEntry(TreeNode node) {
    while (node.right != null) {
        node = node.right;
    }
    return node;
}
private static TreeNode getFirstEntry(TreeNode node) {
    while (node.left != null) {
        node = node.left;
    }
    return node;
}

相关题目会持续添加

References

• TreeMapSourceAnalysis