PriorityQueue源码解读

PriorityQueue源码解读

优先队列, 顾名思义就是按照元素的优先级进行弹出等操作, 那么在JDK中使用何种数据结构来实现优先队列嘞, Let’s Go

依赖

PriorityQueue

emmm, 感觉从依赖上来看, 和其他的集合类一样, 实现其对应的接口(Marker Interface的作用?)

基础

在阅读基础的时候，我们需要先理解一下什么是堆，其数据结构是啥，有哪些存储方式。

1. 堆的底层数据结构为完全二叉树
2. 存储方式（既然是二叉树，那么其存储方式主要分为如下两种）
   1. 顺序存储结构
      1. 根节点下标为0
      2. 若节点p的下标为$i$，则左孩子$2\cdot i$ 右孩子为$2 \cdot i + 1$
      3. 若节点p的下标为$i$，则父节点的下标为$\lfloor i/2\rfloor$
   2. 链式存储结构

树的存储结构

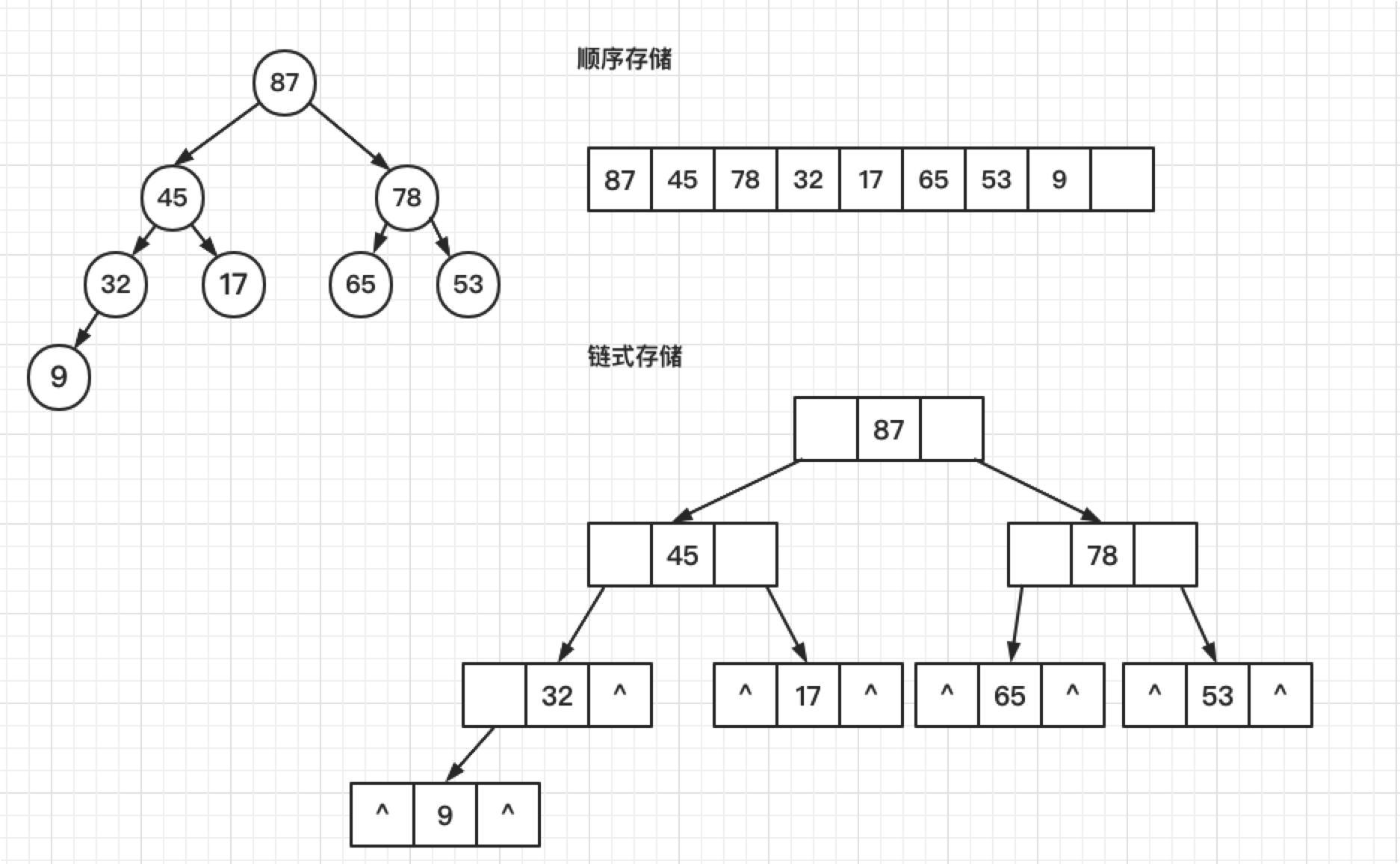
由上述的顺序存储结构可知，堆是用物理上的线性表示逻辑上的非线性的数据结构

具体的关于堆的操作，如刚开始的建堆，以及插入元素，删除堆顶元素，迭代等操作，可自行百度。

属性

// 默认初始化容量
private static final int DEFAULT_INITIAL_CAPACITY = 11;
// 底层使用Object[]数组实现, 和ArrayList这些一样
transient Object[] queue; // non-private to simplify nested class access
// 标记元素个数
private int size = 0;
// 比较器, 说明其实例均是可比较的
private final Comparator<? super E> comparator;
// 说明具有fast fail 机制
transient int modCount = 0; // non-private to simplify nested class access

因为底层使用的是数组，同时其本身是支持动态插入和删除的，所以同理，和ArrayList同理，扩容应该是其核心的地方。同时也要关注其是否生成新的数组对象。

像ArrayList、HashMap中都有一个属性叫 modCount，每次对集合的修改这个值都会加1，在遍历前记录这个值到 expectedModCount中，遍历中检查两者是否一致，如果出现不一致就说明有修改，则抛出ConcurrentModificationException异常。

构造函数

PriorityQueue()

public PriorityQueue() {
    this(DEFAULT_INITIAL_CAPACITY, null);
}

PriorityQueue(int initialCapacity)

public PriorityQueue(int initialCapacity) {
    this(initialCapacity, null);
}

PriorityQueue(Comparator<? super E> comparator)

public PriorityQueue(Comparator<? super E> comparator) {
    this(DEFAULT_INITIAL_CAPACITY, comparator);
}

PriorityQueue(int initialCapacity, Comparator<? super E> comparator)

public PriorityQueue(int initialCapacity,
                     Comparator<? super E> comparator) {
    // Note: This restriction of at least one is not actually needed,
    // but continues for 1.5 compatibility
    if (initialCapacity < 1)
        throw new IllegalArgumentException();
    this.queue = new Object[initialCapacity];
    this.comparator = comparator;
}

还有几个构造函数主要是用于将原各种类型的数据放入PriorityQueue中

增(入队)

在阅读这些方法的时候, 想起来自己手撕算法的时候, 经常会记混List, Stack, Queue, Map这些的添加删除操作的API…

下面罗列的是个人觉得不错的代表数据结构特性的添加/删除操作的API

数据结构	添加	删除
List/Set	add()	remove()
Stack	push()	pop()
Queue	offer()	poll()
Map	put()	remove()

用于入队的操作有add和offer。

public boolean add(E e) {
    return offer(e);
}

public boolean offer(E e) {
      // 不支持null元素
    if (e == null)
        throw new NullPointerException();
    modCount++;
    int i = size;
    // 元素数量超过数组数量，引发扩容机制
    if (i >= queue.length)
        // 扩容机制先按下不表
        grow(i + 1);
    // 元素数量+1
    size = i + 1;
      // 如果还没有元素
    // 直接插入到数组第一个位置
    if (i == 0)
        queue[0] = e;
    else
        // 否则 插入到堆的最后一个元素
        // 然后再调整堆
        siftUp(i, e);
    return true;
}

宏观上来看, offer()方法会先检测是否需要扩容, 之后再插入元素, 最后进行调整, 最后调用siftUp进行调整。

siftUp

假设在数组queue的k位置插入元素key（小根堆）

• 不断的比较key和k的父节点e （$queue\lfloor(k-1/2\rfloor)$）的关系
  1. 若$key < e$ ，则queue[k] = e, 同时k到达e的位置（parent）
  2. 若$key \geq e$ 或者 $k$已经到达跟节点，则结束循环
• $queue[k]==e$

private void siftUp(int k, E x) {
    // 判断比较策略
    // 1. X自身实现了Comparable接口，则通过comparable进行比较
    // 2. X自身未实现Comparable接口，通过自定义的外部比较器compartor比较
    if (comparator != null)
        siftUpUsingComparator(k, x);
    else
        siftUpComparable(k, x);
}
@SuppressWarnings("unchecked")
private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (key.compareTo((E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = key;
}
@SuppressWarnings("unchecked")
private void siftUpUsingComparator(int k, E x) {
    while (k > 0) {
        int parent = (k - 1) >>> 1;
        Object e = queue[parent];
        if (comparator.compare(x, (E) e) >= 0)
            break;
        queue[k] = e;
        k = parent;
    }
    queue[k] = x;
}

结论

1. 不允许null元素
2. 插入元素前，先检测数组长度是否够用，不够进行扩容（扩容机制后续详细阐述）
3. 在尾部插入元素，之后不断调整
4. 通过调整的过程，可以知道PrioriryQueue默认是小根堆

删(出队)

出队有两个方法，poll()和remove()，实际上remove调用的还是poll。remove不存在的元素时会报错。

public E remove() {
    E x = poll();
    if (x != null)
        return x;
    else
        throw new NoSuchElementException();
}

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];
    // 获取当前最后一个元素
    // 并将最后一个位置置空
    E x = (E) queue[s];
    queue[s] = null;
    // 如果弹出元素后还有元素
    if (s != 0)
        //将队列末元素移到队列首
        // 再做自上而下的堆化
        siftDown(0, x);
    return result;
}

siftDown

自顶向下，选择小的节点，不断的比较、交换，直到：

1. 下标越界
2. 节点的值同时小于等于左孩子和右孩子

假设数组queue最后一个元素的值为key（小根堆），下标k从0开始，当k存在左孩子时，执行以下循环：

• 若k有右孩子，则比较左右孩子的值，然后选出小的孩子child
• 比较key和c=queue[child]的大小
  1. 若$key \leq c$ 结束循环
  2. 若$key > c$, 则$queue[k] = c, k = child$， 继续循环
• $queue[k] = key$

private void siftDown(int k, E x) {
    // 和 siftUp一样的思路
    if (comparator != null)
        siftDownUsingComparator(k, x);
    else
        siftDownComparable(k, x);
}
@SuppressWarnings("unchecked")
private void siftDownComparable(int k, E x) {
    // 因为删除是从堆顶开始删除，所以和siftUp相反
    Comparable<? super E> key = (Comparable<? super E>)x;
    int half = size >>> 1;        // loop while a non-leaf
    while (k < half) {
        int child = (k << 1) + 1; // assume left child is least
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
            c = queue[child = right];
        if (key.compareTo((E) c) <= 0)
            break;
        queue[k] = c;
        k = child;
    }
    queue[k] = key;
}
@SuppressWarnings("unchecked")
private void siftDownUsingComparator(int k, E x) {
    int half = size >>> 1;
    while (k < half) {
        int child = (k << 1) + 1;
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            comparator.compare((E) c, (E) queue[right]) > 0)
            c = queue[child = right];
        if (comparator.compare(x, (E) c) <= 0)
            break;
        queue[k] = c;
        k = child;
    }
    queue[k] = x;
}

1. 将队列首元素弹出
2. 将队列末元素移到队列首
3. 自上而下堆化，一直往下与最小的子节点比较
4. 如果比最小的子节点大，就交换位置，再继续与最小的子节点比较
5. 如果比最小的子节点小，就不用交换位置了，堆化结束

获取队头元素

public E peek() {
    return (size == 0) ? null : (E) queue[0];
}

获取第一个元素的值。

扩容策略

private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;
private void grow(int minCapacity) {
    int oldCapacity = queue.length;
    // Double size if small; else grow by 50%
    int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                     (oldCapacity + 2) :
                                     (oldCapacity >> 1));
    // overflow-conscious code
    // 检查是否溢出
    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);
    queue = Arrays.copyOf(queue, newCapacity);
}
private static int hugeCapacity(int minCapacity) {
    if (minCapacity < 0) // overflow
        throw new OutOfMemoryError();
    return (minCapacity > MAX_ARRAY_SIZE) ?
        Integer.MAX_VALUE :
        MAX_ARRAY_SIZE;
}

1. 原数组空间大小<64时，默认扩容为原先的两倍再加2个。。。
2. 原数组空间大小>64时，扩容为原先的1.5倍
3. 最大容量空间为Integer.MAX_VALUE

总结

1. PriorityQueue内部的数据结构是堆，堆使用的数据结构是完全二叉树，然后使用的是顺序存储结构（数组）
2. PriorityQueue默认是小根堆
3. 堆保证堆顶元素为当前的最值，然后严格遵守字节点的值大于（小于）父节点的值
4. 堆的删除操作从堆顶进行删除，然后会将最后的一个元素移至堆顶，此时堆的结构被破坏，所以需要执行siftDown
5. 堆的插入操作从堆尾进行插入，此时堆的结构被破坏，所以需要执行siftUp