前言

LeetCode死磕系列一： 二叉树

二叉树其自身就具有递归属性， 所以按道理，绝大多数题目用递归都是可以的

一般情况下:如果需要搜索整颗二叉树，那么递归函数就不要返回值，如果要搜索其中一条符合条件的路径，递归 函数就需要返回值，因为遇到符合条件的路径了就要及时返回

常用操作

  1. 遍历

    1. 前序遍历

      //递归前序遍历
public void preOrder(TreeNode root) {
    if (Objects.isNull(root)) {
        return;
    }
    // do something
    preOrder(root.left);
    preOrder(root.right);
}
//递归前序遍历
public void preOrder(TreeNode root) {

}
//非递归前序遍历
public void preOrderII(TreeNode root) {
    if (Objects.isNull(root)) {
        return;
    }
    Deque<TreeNode> stack = new ArrayDeque<>();
    TreeNode p = root;
    while (!stack.isEmpty() || p != null) {
        while (p != null) {
            // do something
            stack.push(p);
            p = p.left;
        }
        if (!stack.isEmpty()) {
           p = stack.pop();
           p = p.right;
        }
    }
}

    2. 中序遍历

      //递归中序遍历
public void inOrder(TreeNode root) {
    if (Objects.isNull(root)) {
        return;
    }
    inOrder(root.left);
    // do something
    inOrder(root.right);
}
//非递归中序遍历
public void inOrderII(TreeNode root) {
    if (Objects.isNull(root)) {
        return;
    }
    TreeNode p = root;
    Deque<TreeNode> stack = new ArrayDeque<>();
    while (!stack.isEmpty() || p != null) {
        while (p != null) {
            stack.push(p);
            p = p.left;
        }
        if (!stack.isEmpty()) {
            p = stack.pop();
            // do something
            p = p.right;
        }
    }
}

  1. 后序遍历

    //递归后序遍历
public void postOrder(TreeNode root) {
    if (Objects.isNull(root)) {
        return;
    }
    postOrder(root.left);
    postOrder(root.right);
    // do something
}
//非递归后序遍历
public void postOrderII(TreeNode root) {
    if (Objects.isNull(root)) {
        return;
    }
    Deque<TreeNode> stack = new ArrayDeque<>();
    Deque<TreeNode> list = new ArrayDeque<>();
    Deque<TreeNode> reverse = new ArrayDeque<>();
    TreeNode p = root;
    stack.push(p);
    while (!stack.isEmpty()) {
        p = stack.pop();
        list.push(p);
        if (p.right != null) {
            stack.push(p.left);
        }
        if (p.left != null) {
            stack.push(p.left);
        }
    }
    while (!list.isEmpty()) {
        reverse.add(list.pop());
    }
}

  2. 层次遍历

    public void levelOrder(TreeNode root) {
    if (Objects.isNull(root)) {
        return;
    }
    Deque<TreeNode> queue = new ArrayDeque<>();
    TreeNode p = root;
    queue.offer(p);
    while (!queue.isEmpty()) {
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            p = queue.poll();
            if (p.left != null) {
                queue.offer(p.left);
            }
            if (p.right != null) {
                queue.offer(p.right);
            }
        }
    }
}

  1. 公共祖先

  2. 树转链表

  3. 重新构建二叉树

  4. 路径之和

  5. 深度和高度

    1. 求二叉树深度 和 二叉树高度的差异，求深度适合用前序遍历，而求高度适合用后序遍历
    2. 因为深度可以从上到下去查 所以需要前序遍历(根左右)，而高度只能从下到上去查，所以只能后序遍历(左右根)

LeetCode&剑指offer 二叉树题目整理

  1. 二叉树的前序遍历

  2. 二叉树的中序遍历

  3. 二叉树的后序遍历

    1. 二叉树的高度
    2. 二叉树的直径
    3. 二叉树的深度

  4. 二叉树的层次遍历

    层次遍历能解决很多关于二叉树的问题，目前根据考研经验以及LeetCode刷题总结，其作用范围大概如下：

    1. 二叉树的深度
      1. 最大深度
        1. 一次正常的层次遍历
      2. 最小深度
        1. 第一次遇到当前节点为叶子节点时遍历结束
    2. 二叉树的宽度
      1. 最大宽度
      2. 最小宽度

    以上两道题可以感觉出，层次遍历将二叉树定在了一个二维的坐标轴上，二叉树的层为一个方向，深度为一个方向。只要是和层和深度相关的内容都可以考虑试试层次遍历。以下的内容也都是在层和深度的基础上的一些小变化（最直白的简单题）

    1. 每一层的平均值、最大值、最小值等
    2. 二叉树的左视图、右视图

    相关变种题目：

    1. 102.二叉树的层序遍历
    2. 107.二叉树的层次遍历II
    3. 199.二叉树的右视图
    4. 637.二叉树的层平均值
    5. 429.N叉树的层序遍历
    6. 515.在每个树行中找最大值
    7. 116.填充每个节点的下一个右侧节点指针
    8. 117.填充每个节点的下一个右侧节点指针II
    9. 104.二叉树的最大深度
      1. 解法不唯一，也可使用后序遍历解决。
    10. 111.二叉树的最小深度
      1. 和上一题一样的思路，但是条件不一样
      2. 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
    11. 222.完全二叉树的节点个数

  5. 路径问题

    1. 是否有满足和为sum的路径
    2. 求所有慢煮和为sum的路径

  6. 构造二叉树

    1. 给定一个数组，构造二叉树/构建平衡二叉树
    2. 根据前序中序、后序中序构建二叉树
    3. 二叉树的序列化

  7. 根据数组判断是否为二叉排序树

  8. 公共节点

题解

二叉树的高度

思路：
  1. 递归
  2. 辅助队列

二叉树的直径

思路：

感觉是二叉树的高度的延伸，思路是和二叉树的高度是类似的。

直径： 以当前节点为基础，然后依次获取当前节点的最大左子树深度L和右子树最大深度R，L+R=D即为结果，然后从每个节点的D中选取最大的即可

private int ans;
public int diameterOfBinaryTree(TreeNode root) {
    if (Objects.isNull(root)) {
        return 0;
    }
    ans = 0;
    depth(root);
    return ans-1;
}
private int depth(TreeNode root) {
    if (Objects.isNull(root)) {
        return 0;
    }
    int left = depth(root.left);
    int right = depth(root.right);
    ans = Math.max(ans, left+right);
    return Math.max(left, right) + 1;
}

二叉树的层次遍历

102.二叉树的层序遍历

层次遍历的基础模板题目

public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> out = new ArrayList<>();
        if (Objects.isNull(root)) {
            return result;
        }
        Queue<TreeNode> queue = new ArrayDeque<>();
        TreeNode p = root;
        queue.offer(p);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for(int i = 0; i < size; i++) {
                p = queue.poll();
                out.add(p.val);
                if (p.left != null) {
                    queue.offer(p.left);
                }
                if (p.right != null) {
                    queue.offer(p.right);
                }
            }
            result.add(out);
            out = new ArrayList<>();
        }
        return result;
    }

107.二叉树的层次遍历II

层次遍历的简单变形，根据list的特性，每次新增一层的结果的时，都在首位插入，即可完成逆序存储

public List<List<Integer>> levelOrderBottom(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        List<Integer> out = new ArrayList<>();
        if (Objects.isNull(root)) {
            return result;
        }
        Queue<TreeNode> queue = new ArrayDeque<>();
        TreeNode p = root;
        queue.offer(p);
        while (!queue.isEmpty()) {
            int size = queue.size();
            for(int i = 0; i < size; i++) {
                p = queue.poll();
                out.add(p.val);
                if (p.left != null) {
                    queue.offer(p.left);
                }
                if (p.right != null) {
                    queue.offer(p.right);
                }
            }
            result.add(0, out);
            out = new ArrayList<>();
        }
        return result;
    }

199.二叉树的右视图

二叉树层次遍历的简单变形。

思路： 每次遍历到当前层的最后一个非空节点的时候，存入到右视图的list中

public List<Integer> rightSideView(TreeNode root) {
    List<Integer> result = new ArrayList<>();
    if (Objects.isNull(root)) {
        return result;
    }
    TreeNode p = root;
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.offer(p);
    while (!queue.isEmpty()) {
        int size = queue.size();
        for (int i = 0; i < size; i++) {
            p = queue.poll();
            // 每一层的最后一个节点
            if (i == size - 1) {
                result.add(p.val);
            }
            if (p.left != null) {
                queue.offer(p.left);
            }
            if (p.right != null) {
                queue.offer(p.right);
            }
        }
    }
    return result;
}

637.二叉树的层平均值

二叉树层次遍历的简单变形。

思路： 求每一层的平均值

429.N叉树的层序遍历

515.在每个树行中找最大值

116.填充每个节点的下一个右侧节点指针

117.填充每个节点的下一个右侧节点指针II

104.二叉树的最大深度

思路1 广度遍历(层次遍历)

public int maxDepth(TreeNode root) {
    if (Objects.isNull(root)) {
        return 0;
    }
    TreeNode p = root;
    Queue<TreeNode> queue = new ArrayDeque<>();
    queue.offer(p);
    int count = 0;
    while (!queue.isEmpty()) {
        int size = queue.size();
        count++;
        for (int i = 0; i < size; i++) {
            p = queue.poll();
            if (p.left != null) {
                queue.offer(p.left);
            }
            if (p.right != null) {
                queue.offer(p.right);
            }
        }
    }
    return count;
}

思路2 深度遍历(后序遍历)

public int maxDepth(TreeNode root) {
    if (Objects.isNull(root)) {
        return 0;
    }
    int left = maxDepthII(root.left);
    int right = maxDepthII(root.right);
    return Math.max(left, right) + 1;
}

111.二叉树的最小深度

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

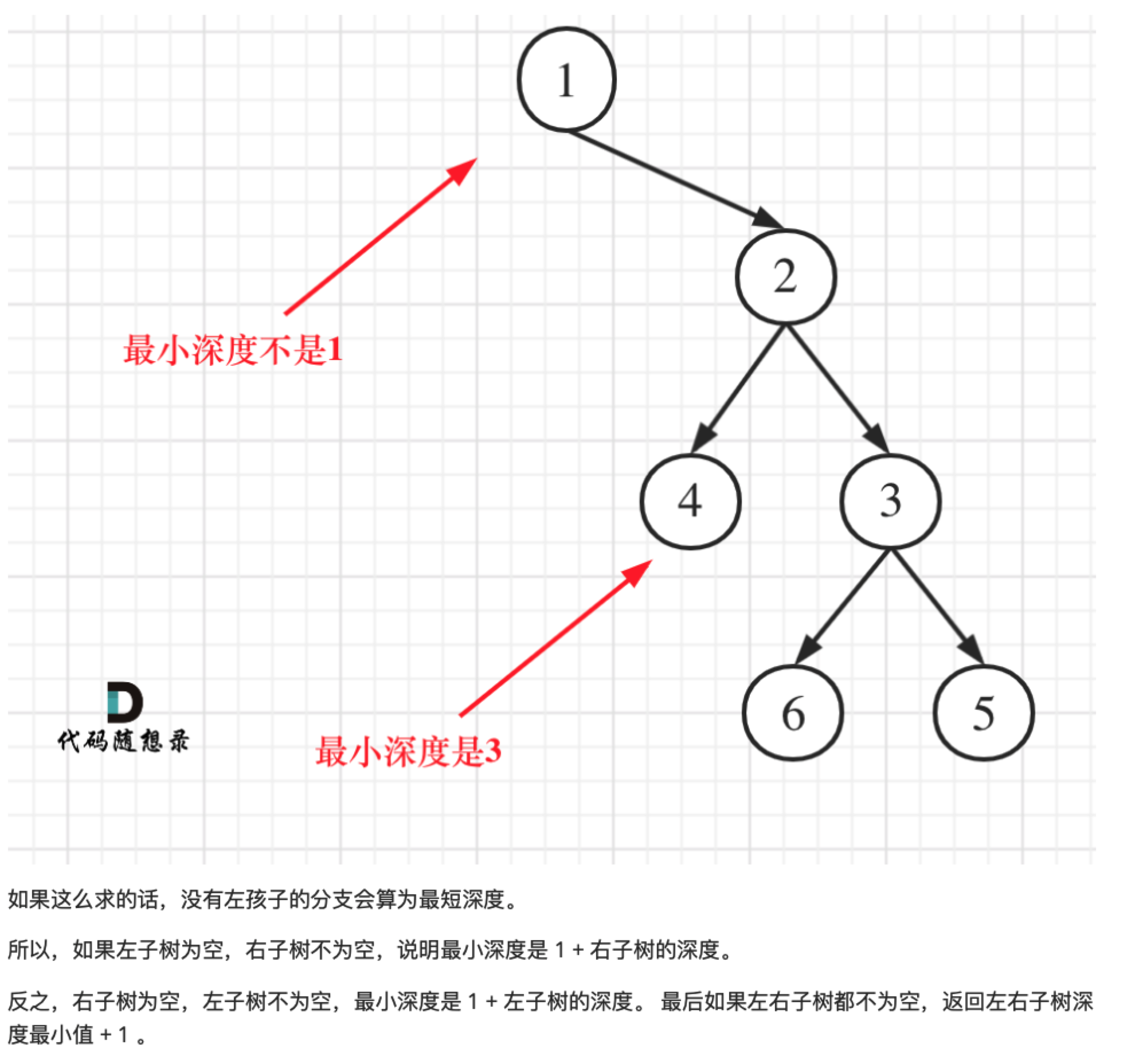
image-20210223220242873
image-20210223220242873
/**
 * 深度遍历（后序）
 * @param root
 * @return
 */
public int minDepth(TreeNode root) {
    if (Objects.isNull(root)) {
        return 0;
    }
    int left = minDepth(root.left);
    int right = minDepth(root.right);
    if (root.left == null && root.right != null) {
        return 1 + right;
    } else if (root.left != null && root.right == null) {
        return 1 + left;
    }
    return Math.min(left, right) + 1;
}
/**
 * 广度遍历（层次）
 * @param root
 * @return
 */
public int minDepthII(TreeNode root) {
    int count = 0;
    if (Objects.isNull(root)) {
        return count;
    }
    Queue<TreeNode> queue = new ArrayDeque<>();
    TreeNode p = root;
    queue.offer(p);
    while (!queue.isEmpty()) {
        int size = queue.size();
        count++;
        for (int i = 0; i < size; i++) {
            p = queue.poll();
            if (p.left != null) {
                queue.offer(p.left);
            }
            if (p.right != null) {
                queue.offer(p.right);
            }
            if (p.left == null && p.right == null) {
                return count;
            }
        }
    }
    return count;
}

222.完全二叉树的节点个数

references