前言

LeetCode死磕系列七： DP

终于轮到了DP, 怎么说类, 感觉自己写DP的题挺玄幻的, 状态好了, 能找出转移方程, 就能瞬间解决, 搞不好还能优化, 状态不好了, 只知道可以用DP, 也只是知道….

的确, 和网上的很多总结类似, 做到后面也感觉DP使用的数学知识就是数学归纳法, 然后还有自身的优化, 譬如大多数情况自底向上的DP往往要比自顶向下的DP实现起来简约且效率高, 也可使用滚动数组将高纬的dp数组降维.

两大特性

  1. 无后效行

    • 一旦f(i,j)确定，就不用关心 “我们如何计算出f(i,j)”。
    • 想要确定f(i,j)，只需要知道f(i-1,j)和f(i,j-1)的值，而至于它们 是如何算出来的，对当前或之后的任何子问题都没有影响。
    • 过去不依赖将来，将来不影响过去 —- 智巅语录

  2. 最优子结构

    1. f(i,j)的定义就已经蕴含了“最优”。

    2. 大问题的最优解可以由若干个小 问题的最优解推出。(max,

      min, sum…)

DP能适用的问题:能将大问题拆成几个小问题，且满足无后效性、最优子结构性质。

题目特点

  1. 计数
    1. 有多少种方式走到右下角
    2. 有多少种方法选出k个数使得和是sum
  2. 求最大值最小值
    1. 从左上角走到右下角路径的最大数字和
    2. 最长上升子序列长度
  3. 求存在性
    1. 取石子游戏，先手是否必胜
    2. 能不能选出k个数使得和是sum

主要类型

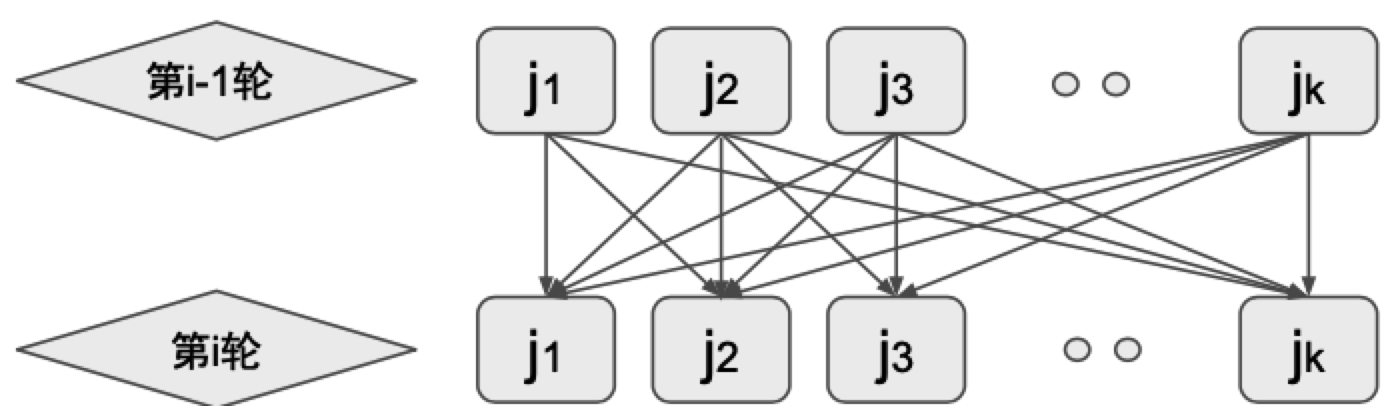
I:时间序列模型

给出一个序列（字符串、数组），其中每一个元素可以认为一天，并且今天的状态只取决于昨天的状态

套路

  • 定义$dp[i][j]$： 表示第i-th轮的第j种状态（j=1,2,3,..k）
  • 千方百计将$dp[i][j]$和前一轮的状态$dp[i-1][j]$产生关系（j=1,2,3,..k）
  • 最后的结果就是$dp[last][j]$的某种操作（sum、max、min…）
image-20210503140232767
image-20210503140232767

II:时间序列加强版(子序列模型)

给出一个序列（数组、字符串），其中每一个元素可以认为一天，但是今天的状态和之前的某一天相关，需要进行挑选

套路

  • 定义$dp[i]$: 表示第i-th轮的状态，一般这个状体要求和元素i直接相关❓
  • 千方百计的将$dp[i]$与之前的状态$dp[i’]$产生关系（i=1,2,3..i-1）操作如（sum、max、min）
    • $dp[i]$肯定不能与大于 i的轮次有任何关系，否 则违反了DP 的无后效性。
  • 最终的结果为$dp[i]$中的某一个

image-20210503141804480

III:双序列模型

给出两个序列$S$和$T$ (数组、字符串)，对它们两个搞事情

  • 编辑距离公式

套路：

  • 定于$dp[i][j]$: 表示针对$S[1:i]$和$T[1:j]$的子问题的求解
  • 千方百计将$dp[i][j]$往之前的状态去转移：$dp[i-1][j], dp[i][j-1], dp[i-1][j-1]$
  • 最终的结果为$dp[m][n]$

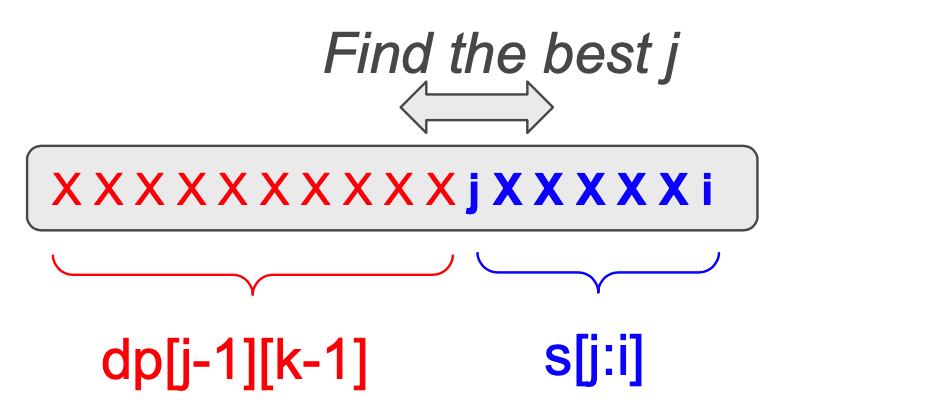
IV:第I类区间型DP

给出一个序列（数组、字符串），明确要求分割成k个连续空间，要你计算这些区间的某个最优性质。

套路

  • 状态定义：$dp[i][k]$表示针对$S[1:i]$分成k个区间，此时能够得到的最优解
  • 搜寻最后一个区间的起始位置$j$，将$dp[i][k]$分割成$dp[j-1][k-1]$和$两个部分
  • 最终的结果是$dp[N][K]$
image-20210503143245100
image-20210503143245100

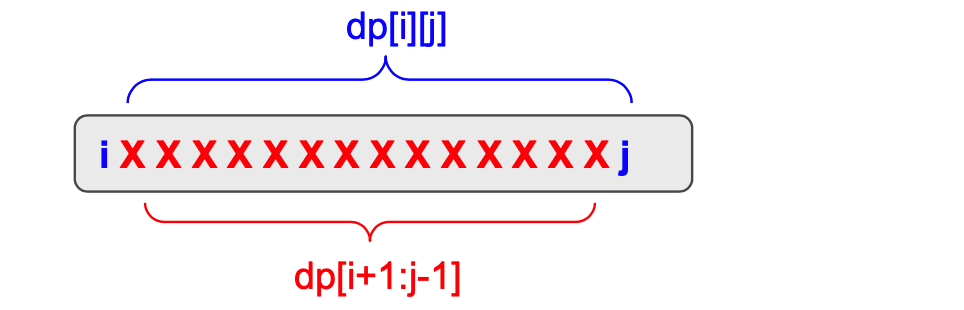
V:第II类区间型DP

只给出一个序列S（数组、字符串），求一个针对这个序列的最优解

适合条件： 这个最优解对于序列的index而言，没有“无后效性”。即无法设计$dp[i]$使得 $dp[i]$仅依赖于$dp[j] (j<i)$. 但是大区间的最优解，可以依赖小区间的最优解。

套路：

  • 定义$dp[i][j]$:表示针对$s[i:j]$的子问题的求解。
  • 千方百计将最大区间的$dp[i][j]$往小区间的$dp[i’][j’]$转移
    • 第一层循环是区间大小；第二层循环是起始点
  • 最终的结果是$dp[1][N]$
image-20210503144732050
image-20210503144732050

VI:背包入门

题目抽象：给出N件物品，每个物品可用不可用（若干种不同的用法）需要消耗一定的代价。要求以某个有上限C的代价来实现最大收益。（有时候反过来，要求以某个有下限的收益来实现 最小代价。）

套路：

  • 定义$dp[i][j]$表示只从前i件物品的子集里面选择、代价为$j$的最大收益
    • j = 1、2、3、4…C
  • 千方百计的将$dp[i][j]$往$dp[i-1][j’]$转移：考虑如何使用物品i，对代价/收益的影响
    • 第一层建议循环物品
    • 第二层建议循环容量/代价
  • 最后的结果$max{dp[N][c]} | c \in {1,2,..c}$

LeetCode&Offer DP题目整理(按照上述的分类整理)

牢记动归的步骤：

  1. 确定dp的数组和下标的含义
  2. 确定递归公式
  3. dp数组的初始化
  4. 确定遍历顺序
  5. 列举dp数组

时间序列模型❌

  1. 198. 打家劫舍 ✅
  2. 213. 打家劫舍 II ✅
  3. 337. 打家劫舍 III ✅
  4. 121. 买卖股票的最佳时机 ✅
  5. 122. 买卖股票的最佳时机 II✅
  6. 123. 买卖股票的最佳时机 III✅
  7. 188. 买卖股票的最佳时机 IV✅
  8. 309. 最佳买卖股票时机含冷冻期
  9. 376. 摆动序列
  10. 487. 最大连续1的个数 II✅
  11. 1186. 删除一次得到子数组最大和✅
  12. 714. 买卖股票的最佳时机含手续费
  13. 剑指 Offer 63. 股票的最大利润

时间序列模型加强版(子序列问题)✅

  1. 300. 最长递增子序列✅
  2. 368. 最大整除子集✅

双序列模型✅

备注：设置dp空间是，看有效位从0还是1开始。

  • 从1开始，是为了让dp转移方程更加具有适用性，能从最开始的字符串就能计算
  • 从0开始，需要额外考虑初始化过程。行、列

题目：

  1. 72. 编辑距离
  2. 32. 最长有效括号
  3. 115. 不同的子序列
  4. 1143. 最长公共子序列
  5. 最长公共子串
  6. 字符串交错组成

区间序列模型

  1. 1278. 分割回文串 III
  2. 813. 最大平均值和的分组

区间序列模型加强版

背包模型

数组系列

  1. 70. 爬楼梯
  2. 746. 使用最小花费爬楼梯
  3. 72. 编辑距离
  4. 198. 打家劫舍
  5. 213. 打家劫舍 II
  6. 337. 打家劫舍 III
  7. 53. 最大子序和
  8. 322. 零钱兑换
  9. 518. 零钱兑换 II
  10. 120 三角形最小路径和
  11. 300 最长上升子序列
  12. 354. 俄罗斯套娃信封
  13. 64 最小路径和
  14. 174 地下城游戏
  15. 不同路径
  16. 不同路径II

题解

时间序列模型❌

198. 打家劫舍 ✅

时间序列模型：其中每一个元素可以认为一天，并且今天的状态只取决于昨天的状态

  1. 定于状态$dp[i][j]$ 表示第i家，偷或不偷 $j\in {0,1}, i \in {N_i}$

  2. 转移方程

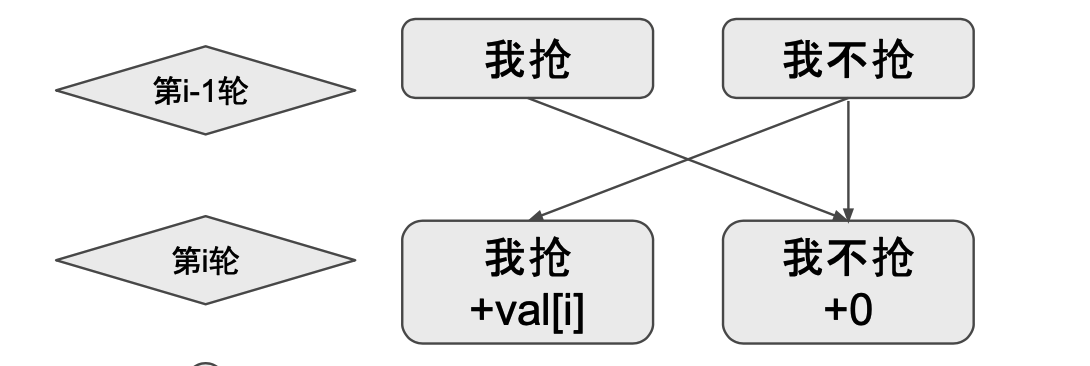
    image-20210503151927577

    • $ dp[i][j]=\left{ \begin{array}{rcl} dp[i][0]= dp[i-1][1] + val[i] && {偷}\ dp[i][1]=Math.max(dp[i-1][0], dp[i-1][1]) &&{不偷}\end{array} \right. $
class Solution {
    public int rob(int[] nums) {
        // 0表示偷
        // 1表示不偷
        int[][] dp = new int[nums.length][2];
        dp[0][0] = nums[0];
        for (int i = 1; i < nums.length; i++) {
            dp[i][0] = dp[i-1][1] + nums[i];
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0]);
            int temp = Math.max(dp[i][0], dp[i][1]);
        }
        int len = nums.length;
        return Math.max(dp[len-1][0], dp[len-1][1]);
    }
}

一维解法

  1. 定义状态

    $dp[i]$表到第i家能偷到的最高金额

  2. 寻找状态转移方程

    1. $dp[0]=nums[0]$ : 目前只有一家, 所以对于小偷来说, 就偷这一家就是最高金额
    2. $dp[1] = Math.max(nums[0], nums[1])$: 目前有两家, 对于小偷来说因为条件限制, 所以只能偷两家中金额最大的那家
    3. $dp[2] = Math.max(dp[0]+nums[2], dp[1])$: 目前有三家, 对于小偷来说因为条件限制, 有两种可能
    4. $dp[3] = Math.max(dp[2], dp[1]+nums[3])$
    5. $dp[i] = Math.max(dp[i-1], dp[i-2]+nums[i])$

  3. 确定边界值

    1. $dp[0] = nums[0]$
    2. $dp[1] = Math.max(nums[0], nums[1])$
public int rob(int[] nums) {
    // TODO 校验
    int[] dp = new int[nums.length];
    dp[0] = nums[0];
    dp[1] = Math.max(nums[1], nums[0]);
    for (int i = 2; i < nums.length; i++) {
        dp[i] = Math.max(dp[i-1], nums[i] + dp[i-2]);
    }
    return dp[nums.length-1];
}

213. 打家劫舍 II ✅

绕圈圈的打家劫舍，在循环数组中打家劫舍，思路是一样的，不过需要分类讨论了（注意数组的边界，可能会出现越界问题）

Trick:首位和末位不能同时抢，这说明至少有一个不能抢。

  1. 考虑首位的房子我不抢，那么对于house[1]~house[last]就是一个基本的 House Robber问题。

  2. 考虑末位的房子我不抢，那么对于house[0]~house[last-1]就是一个基本的 House Robber问题。

class Solution {
    public int rob(int[] nums) {
        // 环形
        // 1. 首位和末位不能同时抢
        // 1.1 首位抢 array[1:N-1];
        // 1.2 末位抢 array[2:N];
        if (nums.length == 1) {
            return nums[0];
        }
        int len = nums.length;
        int first = rob(nums, 0, len - 2);
        int last = rob(nums, 1, len - 1);
        return Math.max(first, last);
    }

    private int rob(int[] nums, int first, int last) {
        int len = last - first + 1;
        if (last == first) {
            return nums[first];
        }
        int[][] dp = new int[len][2];
        // 0 表示偷. dp[i][0] = dp[i-1][0] + val[i];
        // 1 表示不偷 dp[i][1] = max(dp[i-1][0], dp[i-1][1]);
        dp[0][0] = nums[first];
        for (int i = 1; i < len; i++) {
            dp[i][0] = dp[i-1][1] + nums[first + i];
            dp[i][1] = Math.max(dp[i-1][0], dp[i-1][1]);
        }    
        return Math.max(dp[len - 1][0], dp[len - 1][1]);
    }
}

一维解法

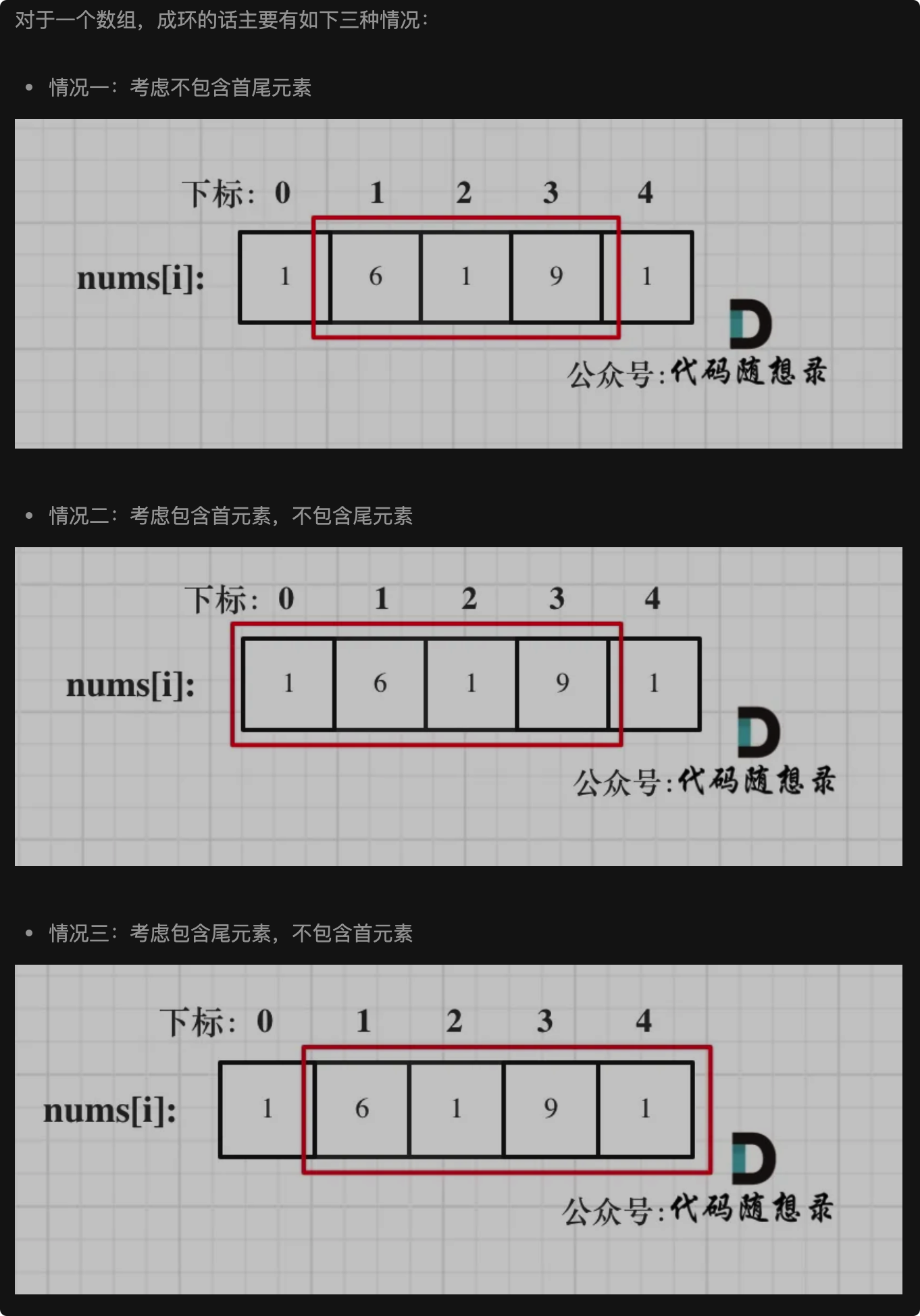
image-20210412181723948
image-20210412181723948

不管是环形的还是正常的数组，数组的位置是不会改变的，所以不会因为偷了i家之后，i-1和i+1就成为邻居了，下次可以考虑在i-1和i+1偷了

public int rob(int[] nums) {
        // dp
        // 定义dp数组和下标含义
        // dp[i] 到第i间房子后，能获取的最大金额
        // dp[i] = Max(dp[i-1],dp[i-2] + nums[i]);
        // 按照分类
        // 1. 小偷偷的房间不包含头尾
        // 2. 小偷偷的房间包含头部
        // 3. 小偷偷的房间包含尾部
        // 1 包含在了2、3两种情况中了
        if (nums == null || nums.length == 0) {
            return 0;
        }
        if (nums.length == 1) {
            return nums[0];
        }
        int left = 0;
        int right = nums.length - 1;
        int first = rob(nums, 0, right - 1);
        int second = rob(nums, 1, right);
        return Math.max(first, second);
    }

    private int rob(int[] nums, int left, int right) {
        if (left == right) {
            return nums[left];
        }
        int len = right - left + 1;
        int[] dp = new int[len];
        dp[0] = nums[left];
        dp[1] = Math.max(nums[left], nums[left + 1]);
        for (int i = 2; i < len; i++) {
            dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i+left]);
        }
        return dp[len-1];
    }

337. 打家劫舍 III ✅

在树上偷。。。

使用后序遍历，已经包含了遍历，所以只需要确定后序面遍历，遍历过程中向上传递什么内容，按照时间序列模型定义，可以直接返回一个二维数组

image-20210503172329150

$ arrayi[2]=\left{ \begin{array}{rcl}array_i[0]=array{left}[1] + array{right}[1] + root.val && {偷}\ array[1]=Max(array{left}[0], array{right}[1]) + Max(arry{right}[0], aray_{right}[1]) &&{不偷}\end{array} \right. $

class Solution {
    public int rob(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int[] array = postOrer(root);
        return Math.max(array[0], array[1]);
    }

    private int[] postOrer(TreeNode root) {
        int[] array = new int[2];
        if (root == null) {
            return array;
        }
        int[] left = postOrer(root.left);
        int[] right = postOrer(root.right);
        // int[] array = new int[2];
        // 0 表示偷 max(left[1], right[1]) + root.val;
        // 1 表示不偷 
        // 向上传递整个array数组
        // 偷当前节点
        int first = root.val+left[1]+right[1];
        // 不偷当前节点
        int second = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        // ans = Math.max()
        array[0] = first;
        array[1] = second;
        return array;
    }
}

121. 买卖股票的最佳时机✅

买卖股票有约束，根据题目意思，有以下两个约束条件：

  • 条件 1：你不能在买入股票前卖出股票；
  • 条件 2：最多只允许完成一笔交易。

因此 当天是否持股 是一个很重要的因素，而当前是否持股和昨天是否持股有关系，所以也为时间序列模型

若是昨天不持股，今天持股，则和第一天持股一个道理，则当前的金额数量为$-V[i]$，最后我们只需要返回最后一天不持股的最大金额数量即可。

image-20210503182851023

$ dp[i][2]=\left{ \begin{array}{rcl}dp[i][0]= Max(dp[i-1][0], -v[i]]) && {持股}\ dp[i][1]=Max(dp[i-1][0] + v[i], dp[i-1][1]) &&{不持股}\end{array} \right. $

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        if (len < 2) {
            return 0;
        }
        // 可以理解为折线统计图，然后求上升最高的线段
        // 不过这次使用动规
        // 0 持股  -prices[i]
        // 1 不持股 +prices[i]
        int[][] dp = new int[len][2];
        dp[0][0] = -prices[0]; // 第0天持股手上的现金
        dp[0][1] = 0; //第0天不持股，手上的现金
        for (int i = 1; i < len; i++) {
            dp[i][0] = Math.max(dp[i-1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i-1][0] + prices[i], dp[i-1][1]);
        }
        return dp[len - 1][1];
    }
}

附加一题剑指 Offer 63. 股票的最大利润，一摸一样。

122. 买卖股票的最佳时机 II ✅

image-20210503192846897

根据上述的转移方式，可以得到如下状态转换

$ dp[i][2]=\left{ \begin{array}{rcl}dp[i][0]= Max(dp[i-1][0], dp[i-1][1]-v[i]]) && {持股}\ dp[i][1]=Max(dp[i-1][0] + v[i], dp[i-1][1]) &&{不持股}\end{array} \right. $

class Solution {
    public int maxProfit(int[] prices) {
        // 动归
        int len = prices.length;
        int[][] dp = new int[len][2];
        // 初始化
        // 0 表示 第i天持有股票
        // 1 表示 第i不持有股票
        dp[0][1] = 0;
        dp[0][0] = -prices[0];
        for (int i = 1; i < len; i++) {
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] + prices[i]);

        } 
        return dp[len-1][1];
    }
}

714. 买卖股票的最佳时机含手续费✅

和上述同理，需要添加手续费

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int len = prices.length;
        // 0 : 持股（买入）
        // 1 : 不持股（售出）
        // dp 定义第i天持股/不持股 所得最多现金
        int[][] dp = new int[len][2];
        dp[0][0] = -prices[0];
        for (int i = 1; i < len; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][0] + prices[i] - fee, dp[i - 1][1]);
        }
        return Math.max(dp[len - 1][0], dp[len - 1][1]);
    }
}

123. 买卖股票的最佳时机 III✅

image-20210503100324818
image-20210503100324818

思路

最高持有两股，分为四种状态

  1. $ dp[i][j]=\left{ \begin{array}{rcl} dp[i][0] = Max(dp[i-1][0], -val[i]) && {第i天，持第有1股的最大利润}\ dp[i][1]=Max(dp[i-1][1], dp[i-1][0] + val[i]) && {第i天，售出第1股的最大收益} \dp[i][2] = Max(dp[i-1][2], dp[i-1][1] - val[i] && {第i天，持有第2股的最大收益} \dp[i][3] = Max(dp[i-1][3], dp[i-1][2] + val[i]) && {第i天，售出第2股的最大收益} \end{array} \right. $

最后的结果为$Max{dp[N][i]} (i = 0, 1, 2, 3)$

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        long[][] dp = new long[n][4];
        // 0 持有1股
        // 1 售出1股
        // 2 持有2股
        // 3 售出2股
        // 第0天 持有一股， 第0天不可能出现售出的现象，只有持有第一股的可能
        dp[0][0] = -prices[0];
        dp[0][2] = -prices[0];
        for (int i = 1; i < n; i++) {
            dp[i][0] = Math.max(dp[i-1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i-1][0] + prices[i], dp[i-1][1]);
            dp[i][2] = Math.max(dp[i-1][1] - prices[i], dp[i-1][2]);
            dp[i][3] = Math.max(dp[i-1][2] + prices[i], dp[i-1][3]);
        }
        long res = 0;
        for(int i = 0; i < 4; i++) {
            res = Math.max(res, dp[n-1][i]);
        }
        return (int)res;
    }
}

188. 买卖股票的最佳时机 IV✅

属于123题的抽象类型，k次买卖，则我们会出现2*k次的持有、售卖状态，然后我们假设偶数为持有股票，奇数为售卖股票

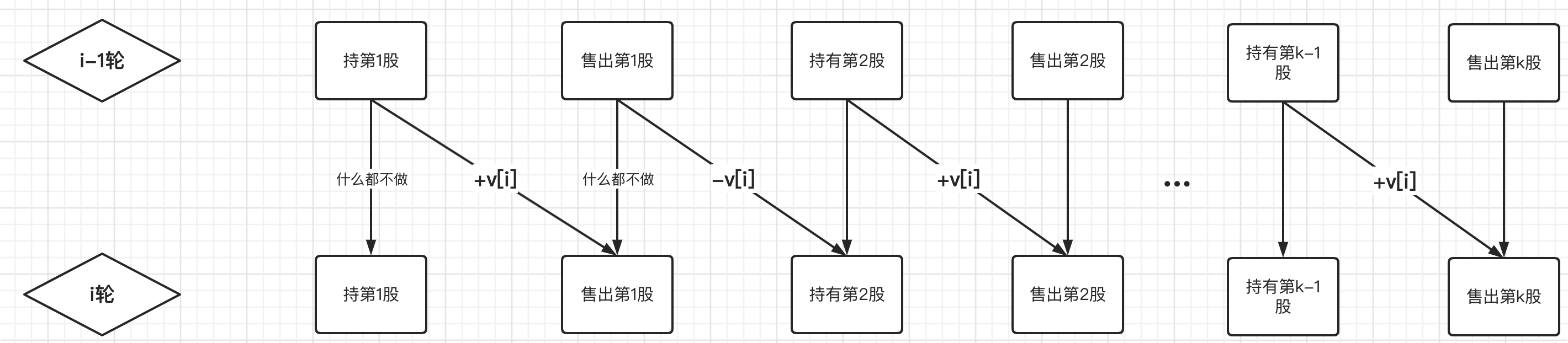
image-20210503202846471
image-20210503202846471
class Solution {
    public int maxProfit(int k, int[] prices) {
        // 类比买卖股票III
        if (prices == null || prices.length == 0) {
            return 0;
        }
        int len = prices.length;
        int[][] dp = new int[len][2*k];
        for (int i = 0; i < 2 * k; i++) {
            if (i % 2 == 0) {
                dp[0][i] = -prices[0];
            }
        }
        for (int i = 1; i < len; i++) {
            for (int j = 0; j < 2 * k ; j++) {
                if (j == 0) {
                    dp[i][j] = Math.max(dp[i-1][0], -prices[i]);
                } else if (j % 2 == 0) {
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-1] - prices[i]);
                } else {
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-1] + prices[i]);        
                }
            }
        }
        // return Arrays.stream(dp[n -1]).max().getAsInt();
        int res = 0;
        for (int i = 0; i < 2 * k; i++) {
            res = Math.max(dp[len-1][i], res);
        }
        return res;
    }
}

309. 最佳买卖股票时机含冷冻期✅

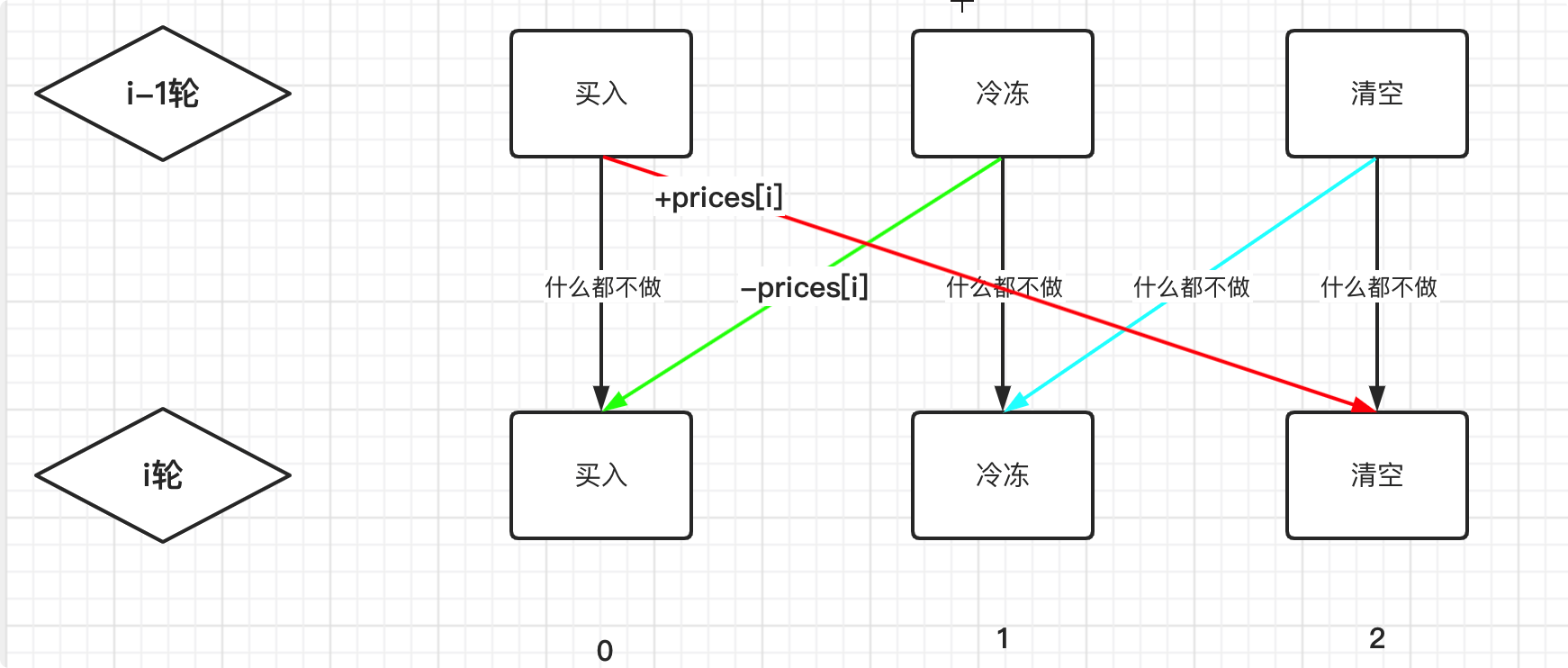
image-20210625160741945
image-20210625160741945

$ dp[i][j]=\left{ \begin{array}{rcl} dp[i][0] = Max(dp[i-1][0], dp[i - 1][1] - priece[i]]) && {第i天，刚持有股票的最大利益}\ dp[i][1]=Max(dp[i-1][1], dp[i-1][2]) && {冷冻的最大收益} \dp[i][2] = Max(dp[i-1][2], dp[i-1][0] + val[i] && {这一轮已经清空股票的最大收益} \end{array} \right. $

class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length;
        if (n < 2) {
            return 0;
        }
        //定义 前i天 不同状态的最大利润
        int[][] dp = new int[n][3];
        // 初始化   
        // 0 : 买入
        // 1 : 冷冻
        // 2 : 清空
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        dp[0][2] = 0;
        for (int i = 1; i < n; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][2]);
            dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][0] + prices[i]);
        }
        return Arrays.stream(dp[n - 1]).max().getAsInt();
    }
}

276. 栅栏涂色

256. 粉刷房子

265. 粉刷房子 II

487. 最大连续1的个数 II✅

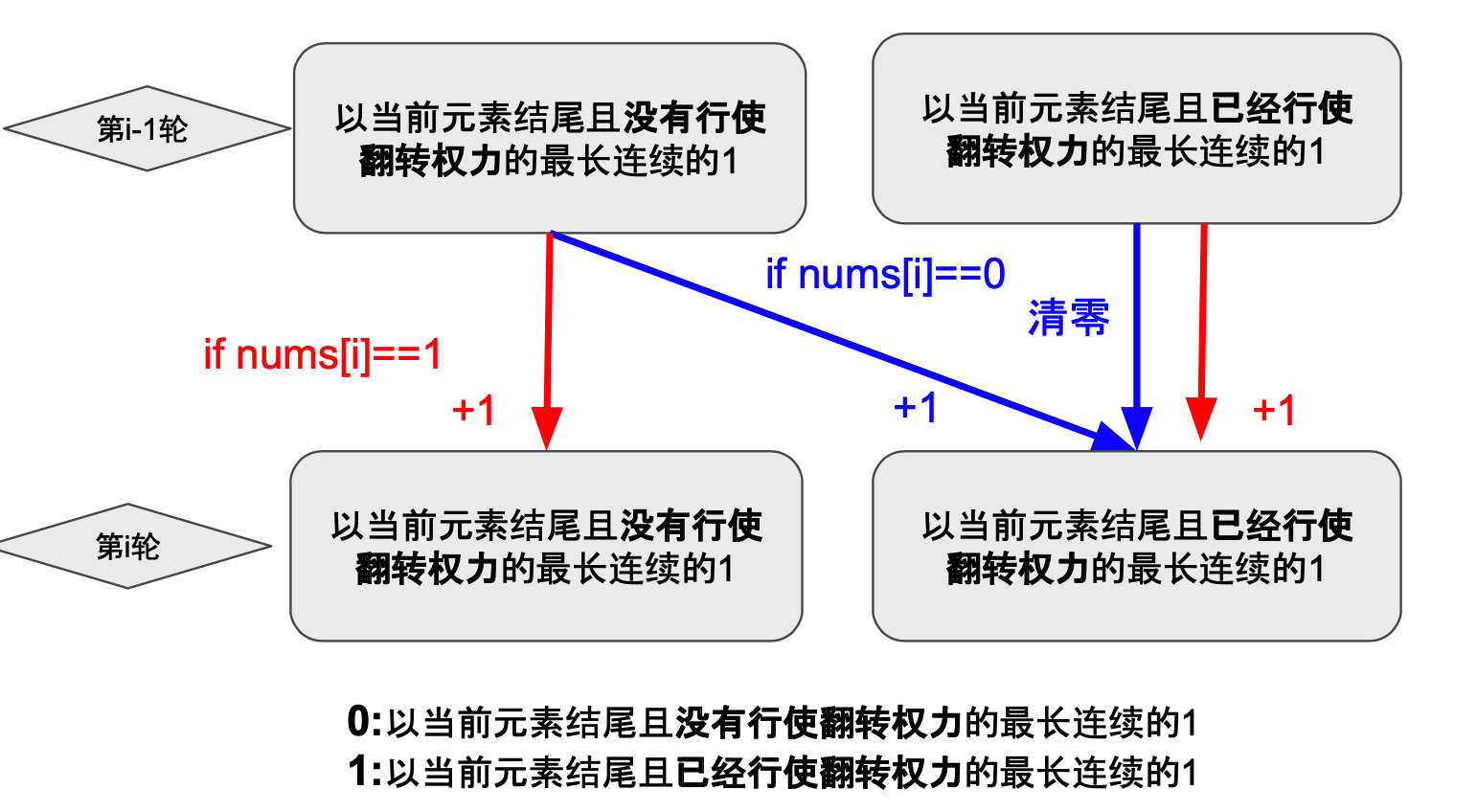
image-20210503235309983
image-20210503235309983
class Solution {
    public int findMaxConsecutiveOnes(int[] nums) {
        int len = nums.length;
        // 以 当前元素为结尾，是否形式翻转权利的最长连续的1
        int[][] dp = new int[len][2];
        // 0 未翻转1
        // 1 翻转1
        dp[0][1] = 1;
        dp[0][0] = nums[0] == 1 ? 1 : 0;
        int ans = Math.max(dp[0][1], dp[0][0]);
        for (int i = 1; i < len; i++) {
            if (nums[i] == 1) {
                dp[i][0] = dp[i-1][0] + 1;
                dp[i][1] = dp[i-1][1] + 1;
            } else {
                dp[i][1] = dp[i-1][0] + 1;
                dp[i][0] = 0; 
            } 
            ans = Math.max(ans, Math.max(dp[i][0], dp[i][1]));
        }
        return ans;
    }
}

1186. 删除一次得到子数组最大和✅

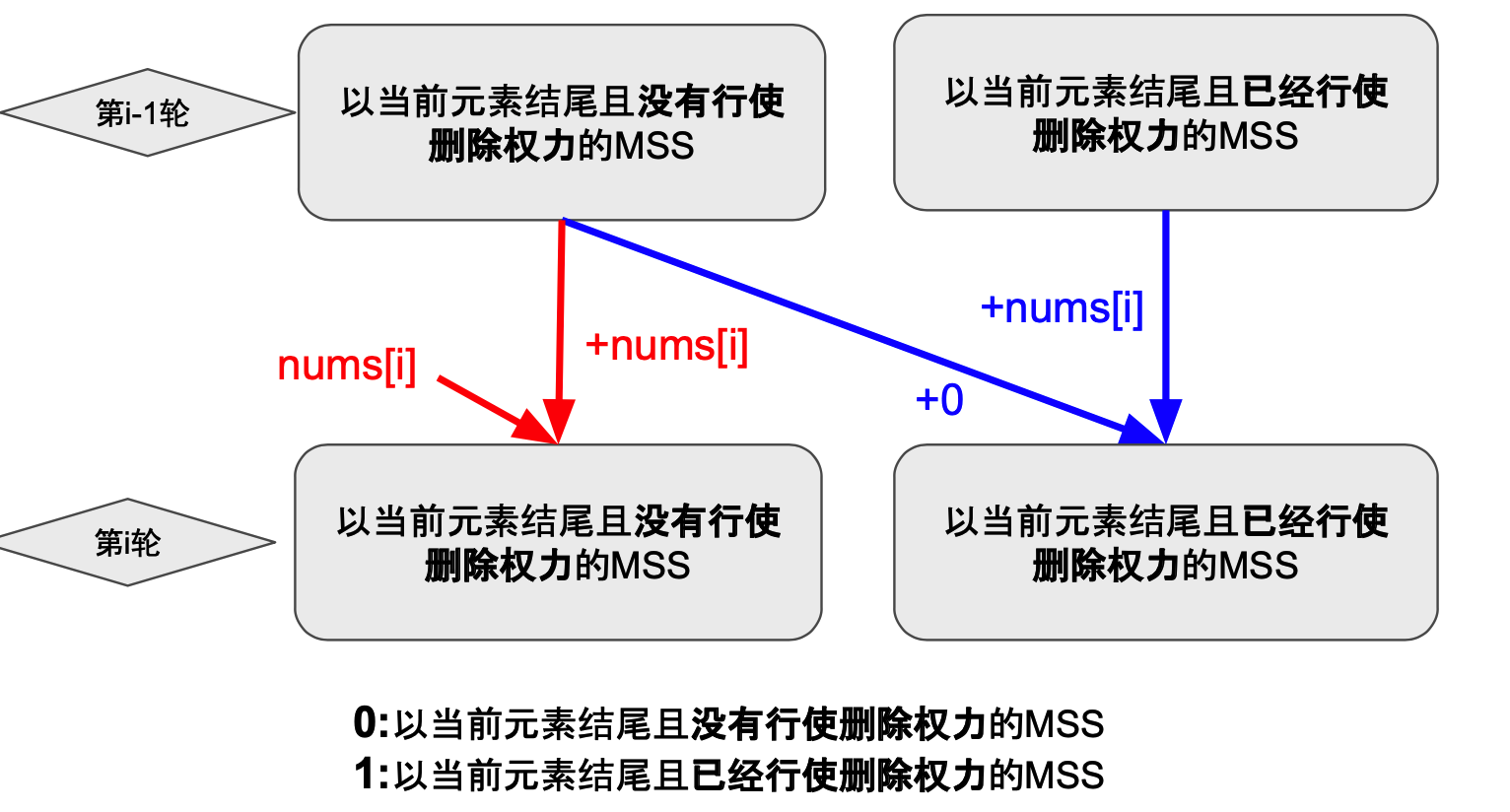
image-20210503235251921
image-20210503235251921
class Solution {
    public int maximumSum(int[] nums) {
        int len = nums.length;
        // 0 不删除
        // 1 删除
        int ans = nums[0];
        int[][] dp = new int[len][2];
        dp[0][0] = nums[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = Math.max(dp[i-1][0]+nums[i], nums[i]);
            dp[i][1] = Math.max(dp[i-1][0], dp[i-1][1] + nums[i]);
            int temp = Math.max(dp[i][0], dp[i][1]);
            ans = Math.max(ans, temp);
        }
        return ans;

    }
}

时间序列模型加强版（子序列模型）✅

300. 最长递增子序列✅

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = nums.length;
        if (len < 2) {
            return len;
        }   
        int[] dp = new int[len];
        Arrays.fill(dp, 1);
        dp[0] = 1;
        int ans = 1;
        for (int i = 1; i < len; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[j] + 1, dp[i]);
                }
            }
            ans = Math.max(dp[i], ans);
        }
        return ans;
    }
}

368. 最大整除子集✅

class Solution {
    public List<Integer> largestDivisibleSubset(int[] nums) {
        int len = nums.length;
        // 第 1 步：动态规划找出最大子集的个数、最大子集中的最大整数
        int[] dp = new int[len];
        Arrays.sort(nums);
        Arrays.fill(dp, 1);
        int maxSize = 1;
        int maxVal = dp[0];
        for (int i = 1; i < len; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] % nums[j] == 0) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);           
                }
            }
            if (dp[i] > maxSize) {
                maxSize = dp[i];
                maxVal = nums[i];
            }
        }

         // 第 2 步：倒推获得最大子集
        List<Integer> res = new ArrayList<Integer>();
        if (maxSize == 1) {
            res.add(nums[0]);
            return res;
        }

        for (int i = len - 1; i >= 0 && maxSize > 0; i--) {
            if (dp[i] == maxSize && maxVal % nums[i] == 0) {
                res.add(nums[i]);
                maxVal = nums[i];
                maxSize--;
            }
        }
        return res;
    }
}

1105. 填充书架

双序列模型✅

区间序列模型

做到现在，其实可以感觉到，对于区间序列模型，其实基本思想是和子序列模型是类似的，不过子序列模型是从前面的多种状态里面获取最优结果，而区间序列是依据前面多种状态+剩余的元素构成的结果 共同决定的最优结果。

1278. 分割回文串 III

明确要求分割成K个连续区间

思路：（经典的区间序列DP）

  1. 首先需要预处理每个区间$[i, j]$变成回文所需修改的字符数量(直接暴力就能获得)， 计为$cost[i,j]$
  2. 设$dp[i][j]$表示前$i$个字符，分为$j$段，最少所需要修改的字符数量，有效字符的下标从$1$开始
  3. 初始时$dp[i,j]$为$+\infty$, $dp[0,0] = 0$
  4. 转移时，枚举前一次的分割点$l \in {0, i-1}$ 这次转移所产生的新的区间为$[l+1, i]$，$dp[i][j] = min(dp[l][j-1] + g(l+1, j))$。
  5. 最终的答案$dp[N][K]$

复杂度分析

  • 预处理需要$O(n^3)$
  • 动态规划需要$O(nk)$空间
  • 总时间复杂度$O(n^3)$
public static int palindromePartition(String s, int _k) {
    int n = s.length();
    s = "#" + s;
    int K = _k;
    int[][] dp = new int[n+1][K+1];
    int[][] cost = new int[n+1][n+1];
    // fill
    for (int[] temp : dp) {
        Arrays.fill(temp, 1000);
    }
    for (int i = 1; i <= n; i++){
        dp[i][1]=calc(s.substring(1, i+1));
    }
    for (int i = 1; i <= n; i++) {
        for (int j = i; j <= n; j++) {
            cost[i][j] = cost[i][j] = calc(s.substring(i, j + 1));
        }
    }
    dp[1][1] = 0;
    for (int i = 1; i <= n; i++) {
        for (int k = 1; k <= Math.min(i, K); k++) {
            for (int l = 0; l <= i - 1; l++) {
                dp[i][k] = Math.min(dp[i][k], dp[l][k-1] + cost[l + 1][i]);
            }
        }
    }
    return dp[n][K];
}
private static int calc(String t) {
    int a = 0;
    int left = 0;
    int right = t.length() - 1;
    while (left < right) {
        if (t.charAt(left) != t.charAt(right)) {
            a++;
        }
        left++;
        right--;
    }
    return a;
}

813. 最大平均值和的分组

本题求“最大值”，一般可以朝DP的方向考虑。另外，题意里有明确的分成k个subarray的要求，大概率就是区间型DP。

套路:

  1. 定义$dp[i][k]$，表示将前$i$个元素分成$k$个subarray的最优解，这里表示前$i$个元素，构成$k$个组，得到的最大平均数的值。突破口就是针对最后一个元素$A[i]$，它必定是在当前的最后一个subarray。
  2. 考虑最后的区间的首元素$j$会在哪里？如果选定了这个位置$j$，那么$dp[i][k]$就分解为了两个子问题，一个是$dp[j-1][k-1]$，是以前已经解决的状态，另一个就是$s[j:i]$这段区间的平均值。两者相加就是$dp[i][k]$.我们搜索所有的$j$的位置，选择使$dp[i][k]$最大化的结果。
public static double largestSumOfAverages(int[] nums, int k) {
    if (nums == null || nums.length == 0) {
        return 0D;
    }
    int len = nums.length;
    // dp[i][j]: 前i个元素，划分为j组，获得的最大平均总值
    double[][] dp = new double[len+1][k+1];
    // 优化 获取前缀和
    //存储前缀和
    double[] prefixSum = getPrefixSum(nums);
    // int[] prefixSum = new int[len + 1];
    // for(int i = 1; i <= len; i++){
    //     prefixSum[i] = prefixSum[i - 1] + nums[i - 1];
    // }
    for (int i = 1; i <= len; i++) { // 元素
        for (int j = 1; j <= Math.min(i, k); j++) { // 组
            if(j == 1){ //针对只有1个分组的情况
                dp[i][j] = (double)prefixSum[i] / i;
                continue;
            }
            for (int l = 0; l <= i - 1; l++) {
                dp[i][j] = Math.max(dp[i][j], dp[l][j-1] + (double)(prefixSum[i] - prefixSum[l]) / (i - l));
            }
        }
    }
    return dp[len][k];
}
private static double[] getPrefixSum(int[] nums) {
    int len = nums.length;
    double[] prefixSum = new double[len + 1];
    for (int i = 1; i <= len; i++) {
        prefixSum[i] = prefixSum[i-1] + nums[i-1];
    }
    return prefixSum;
}

区间序列模型加强版

背包模型

数组系列

70. 爬楼梯

  1. 定义状态:

    $dp[i]$ 代表到达第$i$阶台阶, 有多少种走法

  2. 寻找状态转移方程

    1. $dp[1] = 1$: 到达第1阶台阶只有一种走法$[1]$
    2. $dp[2] = 2$: 到达第2阶台阶有两种走法$[1,1], [2]$
    3. $dp[3] = 3$: 到达第3阶台阶有三种走法$[1,1,1], [1,2], [2, 1]$
    4. $dp[4] = 5$: 到达第4阶台阶有五种走法$[1,1,1,1], [1,1,2],[1,2,1],[2,2][2,1,1]$
    5. 通过上述的推演, 可以归纳, $dp[i]=dp[i-1] + dp[i-2]$, 也就是到达第$i$阶的台阶共有两种可能方式, 第一种是通过第$i-1$阶再走1步, 第二种是通过第$i-2$阶再走2步, 同时到达第$i-1$阶的走法有$dp[i-1]$种, 到达第$i-2$阶的走法有$dp[i-2]$种, 则$dp[i] = dp[i-1] + dp[i-2]$

  3. 确定边界值

    刚才找状态转移方程的时候已经确定好了

    1. $dp[1] = 1$
    2. $dp[2] = 2$

因为计算机中, 索引是从0开始的, 如果我们定义长度为n的数组, 则最后一个数组的索引为n-1(我们理解上的dp[n]也就是数组中的dp[n-1]), 则我们定义的边界值$dp[0] = 1$, $dp[1] = 2$, 同理, 若是想直接返回dp[n], 则我们就需要将索引为0的数组元素空出来, 也就是dp[0] = 0, dp[1] = 1, dp[2] = 2

public int climbStairsI(int n) {
    if(n <= 2){
        return n;
    }
    int[] dp = new int[n];
    dp[0] = 1;
    dp[1] = 2;
    for(int i = 2; i<n; i++){
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n-1];
}

public int climbStairsII(int n) {
    if(n <= 2){
        return n;
    }
    int[] dp = new int[n+1];
    dp[0] = 0;
    dp[1] = 1;
    dp[2] = 2;
    for(int i = 3; i<=n; i++){
        dp[i] = dp[i-1] + dp[i-2];
    }
    return dp[n];
}

最后优化

因为我们上述的算法, 消耗了$O(n)$的空间, 同时我们能感觉到可以使用累加的方式进行计算, 而且也只需要返回最终结果, 中间结果我们没必要存储起来, 所以可以做加法运算

public int climbStairs(int n) {
    if(n <= 2){
        return n;
    }
    int a = 1;
    int b = 2;
    int temp;
    for(int i = 3; i<=n; i++){
        temp = a + b;
        a = b;
        b = temp;
    }
    return b;
}

746. 使用最小花费爬楼梯

$ f[i] = cost[i] + min(f[i+1], f[i+2])$

public int minCostClimbingStairs(int[] cost) {
    int f1 = 0, f2 = 0;
    for (int i = cost.length - 1; i >= 0; --i) {
        int f0 = cost[i] + Math.min(f1, f2);
        f2 = f1;
        f1 = f0;
    }
    return Math.min(f1, f2);
}

73. 编辑距离

  1. 定义状态:

    $dp[i][j]$ 表示A的前i个字符到B的前j个字符之间的编辑距离

  2. 寻找状态转移方程

    我觉得二维的状态, 画在纸上更加的简单明了

    初始化

    过程说明

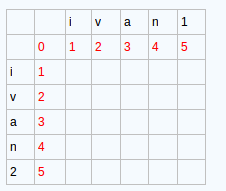
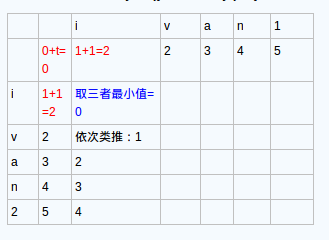
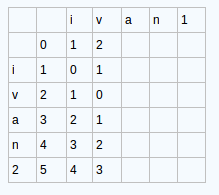
    运行部分结果

    1. $dp[0][j]$表示一个空字符串A到B的前j个字符之间的距离
    2. $dp[i][0]$表示一个空字符串B到字符串A的前i个字符之间的距离
    3. $d[i,j]=min(d[i-1,j]+1 、d[i,j-1]+1、d[i-1,j-1]+temp)$ 这三个当中的最小值
      1. $str1[i] == str2[j]$，表示相同, 用temp记录它，为0。否则temp记为1
      2. $dp[i-1][j]$ 表示增加操作
      3. $dp[i][j-1]$表示删除操作
      4. $dp[i-1][j-1] + temp$表示替换操作

  3. 边界值

    1. $dp[i][0]$
    2. $dp[0][j]$
public static int minDistance(String word1, String word2) {
    int m = word1.length();
    int n = word2.length();
    int[][] dp = new int[m+1][n+1];
    dp[0][0] = 0;
    // 初始化dp
    for(int i = 1; i<=m; i++){
        dp[i][0] = dp[i-1][0] + 1;
    }
    for(int j = 1; j<=n; j++){
        dp[0][j] = dp[0][j-1] + 1;
    }
    int temp = 0;
    // 转移方程: dp[i][j] = Math.min(dp[i-1][j-1]+temp,
    //                       dp[i][j-1]+1, dp[i-1][j]+1);
    for(int i = 1; i<=m; i++){
        for(int j = 1; j<=n; j++){
            // 因为我们的数组这只有效位从1开始
            // 所以标记当前遍历到的字符串的位置为i-1|j-1
            if(word1.charAt(i-1) == word2.charAt(j-1)){
                temp = 0;
            }else {
                temp = 1;
            }
            dp[i][j] = Math.min(Math.min(dp[i-1][j], dp[i][j-1]) + 1, dp[i-1][j-1] + temp);
        }
    }
    return dp[m][n];
}

337. 打家劫舍 III

在树上偷。。。

使用后序遍历，定义一个二维数组

  1. dp[0] : 不偷当前节点的结果

    $dp[0] = Math.max(left[0], left[1]) + Math.max(rigth[0] + right[1])$

  2. dp[1]：偷当前节点的结果

    $dp[1] = root.val + left[0] + right[0]$

public int rob(TreeNode root) {
    int[] res = postOrder(root);
    return Math.max(res[0], res[1]);
}
private int[] postOrder(TreeNode root) {
    if (root == null) {
        return new int[2];
    }
    int[] left = postOrder(root.left);
    int[] right = postOrder(root.right);
    int[] res = new int[2];
    // 不偷当前节点
    int first = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
    // 偷当前节点
    int second = root.val+left[0]+right[0];
    res[0] = first;
    res[1] = second;
    return res;
}

53. 最大子序和

322. 零钱兑换

518. 零钱兑换 II

120 三角形最小路径和

300 最长上升子序列

354. 俄罗斯套娃信封

最后的思路和最长上升子序列一样，不过在此之之前需要整理好数据

/**
 * 354 俄罗斯套娃信封
 * 思路： 详见程序员代码面试指南216页
 * @author weikunkun
 * @since 2021/4/2
 */
public class LC_354 {
    public int maxEnvelopes(int[][] envelopes) {
        // 思路
        // 封装一个信封对象，然后按照信封的宽度进行排序 小-大
        // 如果宽度相同，按照高度排序 大到小
        // 之后 对 高度序列 求最长递增子序列即可
        Envelope[] array = genEnvelope(envelopes);
        int[] heights = genHeightArray(array);
        int[] dp = new int[heights.length];
        Arrays.fill(dp, 1);
        int maxNumber = 0;
        for (int i = 0; i < heights.length; i++) {
            int cur = heights[i];
            int j = 0;
            int max = 0;
            while (j < i) {
                if (heights[j] < cur) {
                    max = Math.max(max, dp[j]);
                }
                j++;
            }
            dp[i] = max + 1;
            maxNumber = Math.max(dp[i], maxNumber);
        }
        return maxNumber;
    }
    private Envelope[] genEnvelope(int[][] envelopes) {
        Envelope[] array = new Envelope[envelopes.length];
        int i = 0;
        for (int[] envelope : envelopes) {
            Envelope env = new Envelope(envelope[0], envelope[1]);
            array[i++] = env;
        }
        Arrays.sort(array, new EnvelopComparetor());
        return array;
    }
    private int[] genHeightArray(Envelope[] array) {
        int[] heights = new int[array.length];
        int i = 0;
        for (Envelope envelope : array) {
            heights[i++] = envelope.height;
        }
        return heights;
    }
}
// 构建一个信封对象
class Envelope {
    public int wight;
    public int height;
    public Envelope(int wight, int height) {
        this.wight = wight;
        this.height = height;
    }
}
class EnvelopComparetor implements Comparator<Envelope> {
    @Override
    public int compare(Envelope o1, Envelope o2) {
        return o1.wight != o2.wight ? o1.wight - o2.wight : o2.height - o1.height;
    }
}

64 最小路径和

174 地下城游戏

从下至上，然后每次当前位置的血量，为 dp[i+1][j+1] - dungeon[i][j]

public int calculateMinimumHP(int[][] dungeon) {
        int[][] dp = new int[dungeon.length][dungeon[0].length];
        int rows = dungeon.length;
        int cols = dungeon[0].length;
        dp[rows-1][cols-1] = Math.max(1-dungeon[rows-1][cols-1], 1);
        for (int i = rows-2; i >= 0; i--) {
            dp[i][cols-1] = Math.max(1, dp[i+1][cols-1] - dungeon[i][cols-1]);
        }
        for (int i = cols-2; i >= 0; i--) {
            dp[rows-1][i] = Math.max(1, dp[rows - 1][i + 1] - dungeon[rows-1][i]);
        }

        for (int i = rows - 2; i >= 0; i--) {
            for (int j = cols - 2; j >= 0; j--) {
                int min = Math.min(dp[i+1][j], dp[i][j+1]);
                dp[i][j] = Math.max(1, min - dungeon[i][j]);
            }
        }
        return dp[0][0];
    }

62. 不同路径

public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        dp[0][0] = 1;
        for(int i = 1; i < m; i++) {
            dp[i][0] = 1;
        }
        for (int i = 1; i < n; i++) {
            dp[0][i] = 1;

        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }

63. 不同路径II

public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        if (null == obstacleGrid || obstacleGrid.length == 0 || null == obstacleGrid[0] || obstacleGrid[0].length == 0) {
            return 0;
        }
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        if (obstacleGrid[0][0] == 1) {
            return 0;
        }
        int[][] dp = new int[m][n];
        dp[0][0] = 1;
        for(int i = 1; i < m; i++) {
            if (obstacleGrid[i][0] == 1) {
                dp[i][0] = 0;
                break;
            } else {
                dp[i][0] = 1;
            }
        }
        for (int i = 1; i < n; i++) {
            if (obstacleGrid[0][i] == 1) {
                dp[0][i] = 0;
                break;
            } else {
                dp[0][i] = 1;
            }
        }

        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 0) {
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                } else {
                    dp[i][j] = 0;
                }
            }
        }
        return dp[m-1][n-1];
    }

字符串系列

72. 编辑距离

这个在数组部分已经讲解过了。

32. 最长有效括号

  1. 确定dp数组，和索引下标意义

    $dp[i]$ 表示 以s[i]结尾的最长有效括号

  2. 确定递归公式

    1. s[i]是'('，以它为结尾的子串，肯定不是有效括号子串——dp[i] = 0

    2. s[i]是')'， 以它为结尾的子串，分类讨论

      1. s[i-1] == '('

        dp[i] = dp[i-2] + 1;

      2. s[i-1] == ')'

        s[i-1]的最长子串为dp[i-1], 所以减去得s[i-dp[i-1]-1]

        1. s[i-dp[i-1]-1]不存在或为')'，则s[i]找不到匹配，直接gg——dp[i]=0

        2. s[i-dp[i-1]-1]是'('，与s[i]匹配，有效长度 = 2 + 跨过的dp[i-1]+ 前方的dp[i-dp[i-1]-2]。等一下，s[i-dp[i-1]-2]要存在才行！

          s[i-dp[i-1]-2]存在，dp[i] = dp[i-1] + dp[i-dp[i-1]-2] + 2
          s[i-dp[i-1]-2]不存在，dp[i] = dp[i-1] + 2

public int longestValidParentheses(String s) {
        int maxans = 0;
        int[] dp = new int[s.length()];
        for (int i = 1; i < s.length(); i++) {
            if (s.charAt(i) == ')') {
                if (s.charAt(i - 1) == '(') {
                    dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
                } else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
                    dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
                }
                maxans = Math.max(maxans, dp[i]);
            }
        }
        return maxans;
    }

115. 不同的子序列

这道题感觉和编辑距离公式的思路差不多，不过，没有那么复杂，只需要考虑减这一个步骤即可。

还是那一个例子来说吧：

输入：S="bagbagbag", T="bag"
输出：5
image-20200907231246178
Support/typora-user-images/image-20200907231246178.png

  1. 定义状态

    $dp[i][j]$ 表示为$T$的前$i$个字符可以由$S$的前$j$个字符组成最多的个数

  2. 寻找状态转移方程

    1. $S[i] == T[j]$

      1. 取$S[i]$，那么当前情况总数，应该和字符串$S$的前$i-1$个字符所构成的子序列中出现字符串$T$的前$j-1$个字符的情况总数相等。$dp[i][j] = dp[i-1][j-1]$
      2. 不取$S[i]$,那么当前情况总数，应该和字符串$S$的前$i$个字符所构成的子序列中出现字符串$T$的前$j-1$个字符的情况总数相等。$dp[i][j] = dp[i][j-1]$
        那么$dp[i][j]$应等于这两种情况的和。$dp[i][j] = dp[i-1][j-1] + dp[i][j-1]$

    2. $S[i] != T[j]$

      只有一种情况，和$S[i] == T[j]$的第二种情况是一样的，因为当前不相等，也就不能取（图中蓝色框）。

      $dp[i][j] = dp[i][j-1]$

    3. 状态转移方程

      $ dp[i][j]=\left{ \begin{array}{rcl} dp[i][j] = dp[i-1][j-1] + dp[i][j-1] & & {S[i] == T[j]}\ dp[i][j]=dp[i][j-1] & & {S[i] != T[j]} \end{array} \right. $

  1. 确定边界值

    1. $dp[0][j]=1$，此时表示为T==NULL，也就是空字符串T可以由非空的S组成的最多的个数，很明显为1。
    2. $dp[i][0] = 0$，此时表示为S==NULL，也就是非空字符串T可以由空的字符串S组成的最多的个数，很明显为0。
public int numDistinct(String s, String t) {
    int m = s.length();
    int n = t.length();
    int[][] dp = new int[n + 1][m + 1];
    dp[0][0] = 1;
    for (int i = 1; i <= n; i++) {
        dp[i][0] = 0;
    }
    for (int i = 1; i <= m; i++) {
        dp[0][i] = 1;
    }
    // 注意i和j和题解上的是相反的
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (t.charAt(i - 1) == s.charAt(j - 1)) {
                dp[i][j] = dp[i][j - 1] + dp[i - 1][j - 1];
            } else {
                dp[i][j] = dp[i][j - 1];
            }
        }
    }
    return dp[n][m];
}

1143. 最长公共子序列

思路和编辑距离差不多，编辑距离返回最后的结果，这里需要遍历整个dp矩阵，返回最大。

/**
 * 首先定义好第一行和第一列
 * 假设 行 text2
 * 假设 列 text1
 * 对于行： text1[0] 和text2[i]中任意一位置字符相同，则i-len位置为1
 * 对于列： 同理
 * 非首行和首列： 1. dp[i-1][j]  dp[i][j-1] dp[i-1][j-1]+1 最大
 * @param text1
 * @param text2
 * @return
 */
public int longestCommonSubsequence(String text1, String text2) {
    int[][] dp = new int[text1.length()][text2.length()];
    int max = 0;
    // 初始化行
    // 初始化列
    // 遍历整个
    int rows = dp.length;
    int cols = dp[0].length;
    dp[0][0] = text1.charAt(0) == text2.charAt(0) ? 1 : 0;
    for (int i = 1; i < rows; i++) {
        dp[i][0] = Math.max(dp[i-1][0], text1.charAt(i) == text2.charAt(0) ? 1 : 0);
        max = Math.max(dp[i][0], max);
    }
    for (int i = 1; i < cols; i++) {
        dp[0][i] = Math.max(dp[0][i-1], text1.charAt(0) == text2.charAt(i) ? 1 : 0);
        max = Math.max(dp[0][i], max);
    }
    for (int i = 1; i < rows; i++) {
        for (int j = 1; j < cols; j++) {
            dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
            if (text2.charAt(j) == text1.charAt(i)) {
                dp[i][j] = Math.max(dp[i][j], dp[i-1][j-1] + 1);
            }
            max = Math.max(dp[i][j], max);
        }
    }
    return max;
}

最长公共子串

找到了和公共子串类似的数组，就拿着替代一下

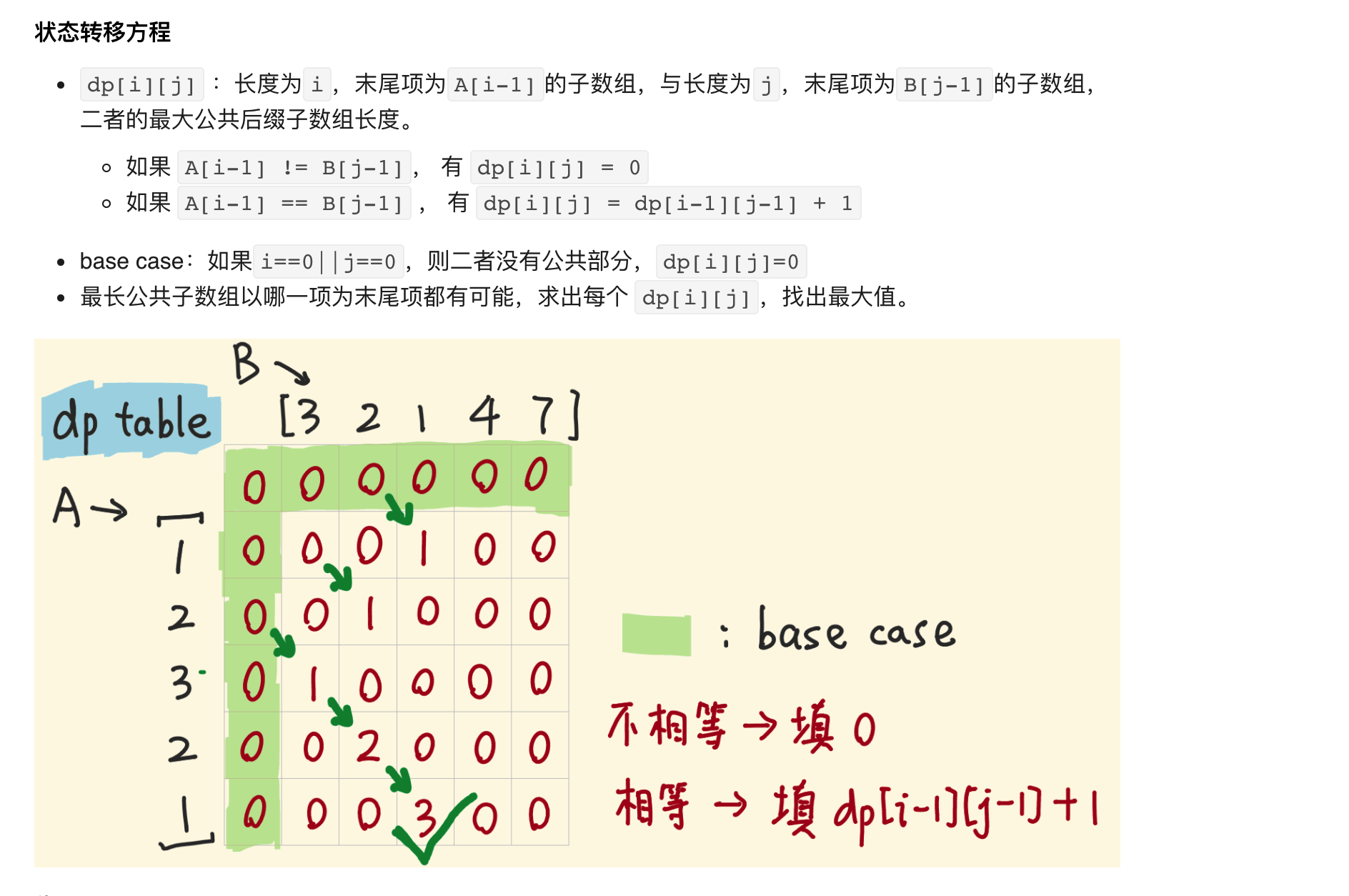
image-20210413155100877
image-20210413155100877
public int findLengthII(int[] nums1, int[] nums2) {
    int len1 = nums1.length;
    int len2 = nums2.length;
    int[][] dp = new int[len1][len2];
    //
    // if nums1[i] == nums2[j]  dp[i][j] = dp[i-1][j-1] + 1;
    // else dp[i][j] = 0;
    int max = 0;
    for (int i = 0; i < len1; i++) {
        if (nums1[i] == nums2[0]) {
            dp[i][0] = 1;
            max = Math.max(max, dp[i][0]);
        }
    }
    for (int i = 0; i < len2; i++) {
        if (nums2[i] == nums1[0]) {
            dp[0][i] = 1;
            max = Math.max(max, dp[0][i]);
        }
    }
    for (int i = 1; i < len1; i++) {
        for (int j = 1; j < len2; j++) {
            if (nums1[i] == nums2[j]) {
                dp[i][j] = dp[i-1][j-1] + 1;
                max = Math.max(dp[i][j], max);
            }
        }
    }
    return max;
}

字符串交错组成

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int n = s1.length(), m = s2.length(), t = s3.length();

        if (n + m != t) {
            return false;
        }

        boolean[][] f = new boolean[n + 1][m + 1];

        f[0][0] = true;
        for (int i = 0; i <= n; ++i) {
            for (int j = 0; j <= m; ++j) {
                int p = i + j - 1;
                if (i > 0) {
                    f[i][j] = f[i][j] || (f[i - 1][j] && s1.charAt(i - 1) == s3.charAt(p));
                }
                if (j > 0) {
                    f[i][j] = f[i][j] || (f[i][j - 1] && s2.charAt(j - 1) == s3.charAt(p));
                }
            }
        }

        return f[n][m];
    }
}